Независимый пружинный блок: Что такое пружинный блок (зависимый и независимый блок пружин)? Характеристики и отзывы о диванах с ортопедическим матрасом

Наполнитель «независимый пружинный блок». Описание

Дата публикации: 25.04.2019

3386

Покупая мягкую мебель большинство людей к сожалению не вникают в суть вопроса, основным критерием является прежде всего стоимость, а потом все остальное, тем самым делая большую ошибку, так разница в цене между ортопедическим матрасом и обычным пружинным не такая уж значительная, тем более если брать в расчет общий срок эксплуатации мебели 7-10 лет, а если учесть тот факт, что во сне человек проводит треть своей жизни, вопрос комфорта и прежде всего собственного здоровья становиться весьма серьезным. 

Для начала давайте попробуем разобраться в чем принципиальная разница между обычным матрасом и с блоком независимых пружин. В обычном блоке, пружины связаны между собой различным образом, повезет еще если это будет BONNEL(Боннель) , принципиальным отличием таких матрасов, является технология изготовления (биконусные пружины радиус витка которых то увеличивается, то уменьшается, каждая пружина сужена в центре и имеет вид песочных часов, скрепляются между собой тонкой проволокой, именно такой необычный вид пружин позволяет равномерно распределить нагрузку). В независимых пружинных блоках каждая пружина помещена в отдельный кокон (чем больше их количество, тем выше ортопедические свойства матраса) сделанный из текстиля и сшитых между собой,  за счет чего достигается эффект точечной гибкости именно это позволяет позвоночнику оставаться в горизонтальном положении, потому что пружины которые не находятся под нагрузкой, остаются в коконах практически без проседания. В большинстве случает сверху блока укладывают пенополиуретан (ППУ), войлок, ватин, кокосовое волокно, латекс и другие материалы которые так же могут повлиять на свойства (сделать матрас более мягким или жестким). 

Отдельно хотелось бы отметить диваны системы аккордеон с независимым пружинным блоком на металлокаркасе, дело в том, что такие системы изготавливаются с ортопедическими латами, из натурального дерева, в сочетании с ортопедическим матрасом получается мебель высочайшего комфорта, благодаря своей компактности, современного дизайна и простоты раскладки (выдвигается на себе при помощи небольшого усилия и с той же легкостью принимает первоначальное положение, при этом образуя идеально ровное спальное место) будет удачным решением при выборе мягкой мебели. Модели с таким механизмом бывают 3-х видов: прямые, угловые и модульные.

Основными преимуществами ортопедического матраса (с независимыми пружинами) является прежде всего здоровый позвоночник, безусловно высокий уровень комфортности, отсутствие скрипучести (так как пружины не взаимодействуют друг с другом) а так же распределение веса происходит таким образом, что любые действия лежащего рядом человека (переворачиваться, ложиться или встает), никак не отразятся на вашем периметре спального места, в отличии от блока зависимых пружин, где из за их связности любое воздействие на определенное место отражается на всей поверхности и последнее, что хотелось отметить, более долгий срок службы, учитывая все вышеперечисленное интернет-магазин «Гост Мебель» советует все таки приобретать мебель с независимыми пружинными блоками, хотя выбор конечно за вами, наши уважаемые покупатели.

Независимый пружинный блок: виды, плюсы и минусы

• Независимый пружинный блок — что это такое?
• Технология производства
• Основные характеристики пружинного блока
• Классификация блоков и их отличия
  • Pocket Spring или TFK
  • Multipocket
  • Micropocket
  • Hour Glass
  • Dual Spring
  • Copper Coil
  • Усиленные
  • С зонами жесткости
• Преимущества и недостатки
• Наполнители для матрасов с независимым пружинным блоком
• Рекомендации по уходу
• Советы по выбору матраса
• Независимый пружинный блок: отзывы покупателей

Полноценный комфортный сон возможен, когда ничто не может его потревожить. Использование матрасов с независимыми пружинными блоками одно из условий, которое гарантирует качественный отдых.

Независимый пружинный блок — что это такое?

Независимый пружинный блок — это уникальная конструкция, собранная по карманной технологии. Каждая пружина цилиндрической, двухконусной или бочонкообразной формы помещается в специальный чехол-карман, что позволяет полностью исключить контакт металлических деталей. Проволочные спирали не соприкасаются друг с другом и сжатие одной не влияет на другие, расположенные рядом. Результат использования технологии карманного типа — отсутствие металлического скрипа при движении во сне и точечное распределение нагрузки на поверхность матраса. Она не прогибается как гамак, что не мешает лежащему рядом человеку.

Матрасы с независимыми пружинными блоками стоят дороже, чем с зависимыми, но за повышенный комфорт принято платить.

Технология производства

Основная особенность независимых пружинных блоков заключается в уникальном принципе соединения пружин. Каждая спираль при объединении в блок остается независимой, не соприкасается с рядом расположенными. Соединение пружин в блоке бесконтактное. Крепятся чехлы, а не проволочные конструкции.

Для получения необходимой жесткости спального места изменяется количество пружин на один квадратный метр.

Среднее число спиралей в отечественных и зарубежных моделях — около 180 штук. В матрасах, изготавливаемых по американским стандартам, возможно 256 пружин на 1 м². Максимальное количество, используемое в изделиях с умеренной или высокой жесткостью — 500 или 1000 шт/м² соответственно.

Основные характеристики пружинного блока

Независимый пружинный блок чутко реагирует на нагрузку, обеспечивает надежную поддержку позвоночнику, сохраняя его в естественном положении, что позволяет полностью расслабиться и дать мышцам отдых.

Чтобы подобрать матрас, который будет идеально отвечать требованиям покупателя, необходимо учитывать несколько критериев, отвечающих за основные характеристики пружинного блока.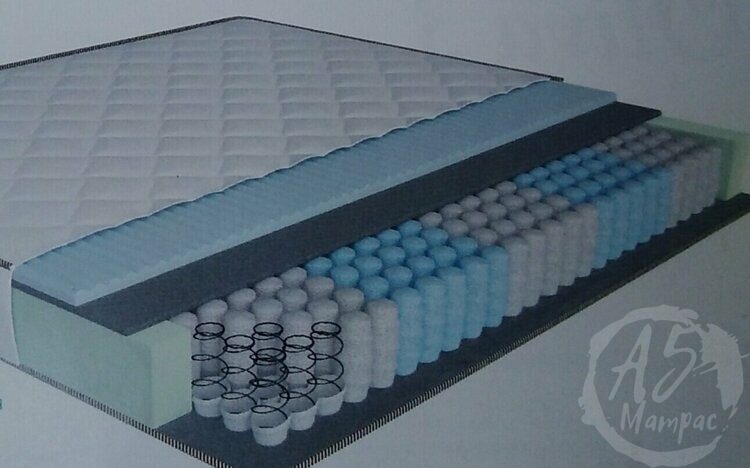

1. Используемая проволока. Необходимо выяснить, какой она толщины, не помешает обратить внимание на качество стали. От указанных параметров зависит, насколько упругой будет пружина и обеспечит ли она необходимую поддержку позвоночника.
2. Количество витков в пружине. Традиционно используют четырех-, пяти- или шестивитковые спирали. Есть модели с большим количеством витков. Чем больше их количество, тем лучше поддержка, которую оказывает пружина.
3. Количество пружин на один кв. метр. Чем больше число спиралей на единицу площади, тем жестче будет поверхность, которую они образуют.
4. Форма спирали. В современных матрасах используются пружины цилиндрической, бочонкообразной и двухконусной (песочные часы) формы.

Пружина «песочные часы» считается одной из самых эффективных для оказания поддержки позвоночника.

Ориентируясь на перечисленные критерии, легко подобрать матрас, который будет отвечать предъявляемым требованиям к комфорту.

Для чего нужен независимый пружинный блок в матрасах в видео:

Классификация блоков и их отличия

В зависимости от количества пружин, их формы и количества на 1 м², различают несколько видов блоков. От их характеристики зависит, насколько комфортно себя будет чувствовать лежащий на матрасе человек.

Pocket Spring или TFK

Один из самых востребованных независимых пружинных блоков. Отличается хорошими ортопедическими характеристиками, обеспечивает оптимальную поддержку позвоночника.

Характеристика пружин:

• диаметр — около 6 см;
• бочонкообразная форма;
• шесть витков;
• 220–300 шт/м².

Удобный блок, отличающийся доступной ценой, что делает его популярным у потребителя.

Multipocket

Блок с отличными анатомическими и ортопедическими свойствами. Характеризуется высокой упругостью и способностью поддерживать тело в его естественном положении.

Характеристика пружин:

• диаметр не более 4-х см;
• цилиндрическая форма;
• количество витков —10–12;
• 500–1000 шт/м², в зависимости от модели.

Единственный недостаток блоков — их высокая цена.

Micropocket

Упругий блок, рассчитанный на очень высокие нагрузки. Рекомендован не только покупателям с большим весом, но и тем, кто предпочитает жесткие поверхности для сна.

Характеристика пружин:

• диаметр — около 2,5 см;
• толщина проволоки — около 1мм;
• количество витков 12–14;
• форма пружины цилиндрическая;
• 500–1000 шт/м².

Блок маловостребован из-за высокой цены.

Hour Glass

Пружинный блок отличается умеренной упругостью, отличными ортопедическими и анатомическими свойствами, которые получены благодаря оригинальной форме спиралей.

Характеристика пружин:

• диаметр — около 6 см;
• количество витков 7,5;
• форма пружин — «песочные часы»;
• не более 300 шт/м².

Именно форма пружин отвечает за основные свойства пружинного блока.

Dual Spring

Пружинный блок с двойными пружинами. Название буквально переводится как «пружина в пружине». Идеально подходит для людей в большой разницей в весе, так как внешние спирали рассчитаны на 100кг нагрузки, а внутренние — на 150 кг.

Характеристика пружин:

• 256 шт/м², внутренних — 128;
• диаметр — около 6 см;
• форма цилиндрическая.

Copper Coil

Блок — усовершенствованный аналог TFK. Отличается расположением пружин, что позволяет увеличить их количество до 300 шт. на 1 м². Эта характеристика позволяет увеличить жесткость матраса.

Усиленные

Особая категория моделей, рассчитанных на нагрузки до 200 кг. В них для пружин используется более упругая проволока, увеличивается количество витков и число спиралей на 1 м².

С зонами жесткости

Специальные модели, имеющие в составе пружины с различными характеристиками. Они распределяются в блоке зонально, что позволяет добиться разной поддержки тела, в зависимости от оказываемого давления на отдельном участке. Такая поддержка позволяет полностью расслабиться и сохранить правильное положение тела во время сна.

Преимущества и недостатки

Любое изделие для сна имеет свои оригинальные характеристики. Как следствие, матрас может иметь ряд достоинств и некоторые недостатки. Чего больше в моделях с независимыми пружинными блоками?

Плюсы

• модели с независимыми пружинами не скрипят в процессе эксплуатации, так как в них не соприкасаются металлические элементы;
• могут использоваться для людей с различным весом, так как в них работает точечное сжатие, и они не создают эффект гамака;
• обеспечивают равномерное распределение нагрузки и сохраняют естественное положение позвоночника;
• позволяют полностью расслабиться и восстановить силы;
• способны выдерживать значительные нагрузки, до 150 (иногда 200) кг;
• имеют длительный срок эксплуатации благодаря прочному чехлу и прочным наполнителям.

Минусы

• единственный недостаток моделей с независимыми пружинными блоками — высокая цена;
• встречаются негативные отзывы о быстром износе изделий (как правило, это вызвано неправильной эксплуатацией матрасов).

Наполнители для матрасов с независимым пружинным блоком

Матрасы с независимыми пружинными блоками отличаются высокой ценой. Чтобы продлить срок их эксплуатации и оправдать заявленную стоимость, необходимо использовать устойчивые к износу наполнители.

Традиционно в таких матрасах используются:

• латекс;
• кокосовая койра;
• струттофайбер;
• ППУ;
• спанбонд;
• термовойлок.

Два последних наполнителя обычно выполняют защитную функцию. Они используются в качестве прослойки между металлическими блоками и мягкими наполнителями.

Рекомендации по уходу

Правильный уход за матрасами существенно продлевает срок их службы. Кроме обычной чистки (для съемных чехлов — стирки), рекомендуется регулярно (один раз в 6 месяцев) переворачивать матрас.

Такой способ эксплуатации позволит равномерно изнашивать стороны изделия и продлевать его службу.

Во избежание появления пылевых клещей или опасных для здоровья бактерий в наполнителях, рекомендуется регулярно проветривать изделие на свежем воздухе. Главное, помнить, что некоторые наполнители не любят открытых солнечных лучей.

Советы по выбору матраса

Чтобы выбрать матрас с независимым пружинным блоком и не ошибиться, рекомендуется не торопиться с покупкой. Отзывы покупателей не всегда могут отражать реальную картину. Известно, что мнения относительно параметров изделия не всегда могут совпадать.

Рекомендуется проконсультироваться с менеджером магазина, лично проверить изделие на жесткость. Если продавцы позволят полежать на матрасе, стоит воспользоваться предложением и лично убедиться, насколько матрас комфортен конкретно для вас.

Только убедившись, что это матрас, на котором вам хотелось бы спать, можно оформлять покупку.

При выборе матраса с независимым пружинным блоком необходимо учесть соответствие параметров матраса весу, потребностям, физическому состоянию человека, для которого он предназначен.

Независимый пружинный блок: отзывы покупателей

Независимые пружинные блоки заслуживают только положительные отзывы. Покупатели говорят об отсутствии скрипа, эффекта волны, удобстве и комфорте. Отмечают, что служат матрасы подолгу без ухудшения качественных характеристик.

Встречаются и негативная реакция на изделия. Покупатели говорят, что при высокой цене сильно страдает качество изделий. При выяснении причин такой реакции выясняется, что эксплуатировалось изделие неправильно или приобреталось у случайных продавцов, не имеющих ничего общего с известными, проверенными производителями.

Хотите получать удовольствие от сна — матрасы с блоком независимых пружин помогут вам насладиться полноценным отдыхом. Ведь независимые пружинные блоки — это полное расслабление, равномерное распределение нагрузки, точечная поддержка позвоночника, отсутствие эффекта волны и скрипа. Главное, приобретать модели в проверенных магазинах или у официальных дилеров производителей.

классическая механика — Почему период пружинного блока не зависит от начального импульса/энергии, подаваемой в систему?

спросил 2 года 5 месяцев назад

Изменено 2 года, 5 месяцев назад

Просмотрено 239 раз

$\begingroup$

Недавно я задавал вопрос о системе пружинных блоков, и меня внезапно смутил тот факт, что независимо от того, с каким импульсом или энергией начинается блок (косвенно насколько сильно сжата пружина), период времени не зависит от Это. Почему это происходит интуитивно?

Причина, по которой я считаю, что период времени независим:

$$ T= 2 \pi \sqrt{\frac{k}{m}}$$

Теперь $ k$ является свойством материала пружины и $ m$ относится к присоединенному блоку, поэтому очевидно, что он не должен зависеть от начальных условий системы.

• классическая механика
• гармонический осциллятор
• пружина

$\endgroup$

2

$\begingroup$

Я имею в виду, что если вы сожмете пружину больше, чем вдавите ее сильнее, тогда у нее будет большее расстояние для перемещения и, следовательно, потребуется больше времени

Интуитивно вы можете думать так: если вы сильнее сожмете пружину, а затем отпустите ее, усилие пружины на блоке будет больше. Следовательно, его ускорение (среднее) выше, благодаря чему он может преодолевать большее расстояние за то же время. 92}{\rm{ (потенциал)}} \end{array}

Лагранжев подход

\begin{array}{l} L = T — V\\ \frac{d}{{dt}}\left( {\frac{{\partial L}}{{\partial \dot x}}} \right) — \frac{{\partial L}}{{\partial х}} = 0\\ \ddot x = — \frac{k}{m}x\\ х = А \ cos \ влево ( {\ омега т} \ вправо) \end{array}

Это говорит мне о периодичности решения и о том, что период не зависит от начальных условий. 2} \\ \dot x = \frac{{\partial H}}{{\partial {p_x}}} = …\\ {{\dot p}_x} = — \frac{{\partial H}}{{\partial x}} = … \конец{массив}

Отсюда было бы ясно, что движение пружины в фазовом пространстве является круговым, поскольку Н постоянна. Если p — ось y, а x — ось x, вы можете представить это круговое движение. Из уравнений движения вы обнаружите, что тангенциальная скорость на этой окружности линейно зависит от количества импульса, который вы ей сообщаете. Если вы придадите ему больше импульса, тангенциальная скорость будет больше, но угловая скорость останется неизменной.

Если вам нужно больше убедительности, вы можете легко смоделировать это самостоятельно, используя временную эволюцию

$$\left( {x,{p_x}} \right) \to \left( {x + \tau \frac{{\partial H}}{{\partial {p_x}}},p — \tau \frac{{\partial H}}{{\partial x}}} \right)$$

Это должно дать вам по крайней мере три веские интуитивные причины, по которым начальное условие (например, импульс) не изменило бы период.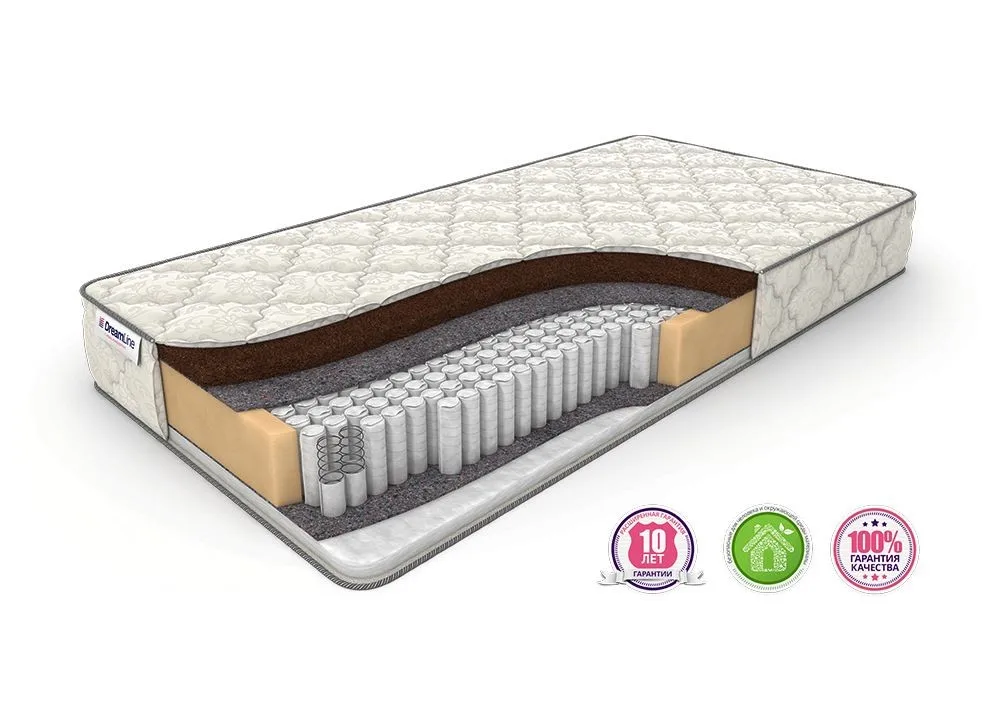

$\endgroup$

2

$\begingroup$

Из закона силы пружины следует: $F = kx$ или $a = (k/m)x$. Важным моментом является то, что ускорение пропорционально расстоянию от центра.

Вы знаете, что одним из решений уравнения является $x = A_1sin(t/T)$

Так почему же $x = A_2sin(t/T)$ также является решением?

Физики ответят, потому что оба решают $F = kx$. Это правильно, но это не дает никакого физического понимания. В общем, физики думают так, потому что уравнения дают вам больше, чем физическое понимание. Особенно когда физика становится нелогичной и очень абстрактной. Но понимание полезно, когда вы можете его получить.

Вот, мы можем получить его. Рассмотрим конкретный пример, где $A_2 = 2A_1$. В каждый момент раствор 2 находится в два раза дальше от центра, чем раствор 1. Закон упругости говорит нам, что сила, притягивающая массу к центру, в два раза больше.

Вы также знаете, что скорость равна $x = (A_{1 или 2}/T)cos(t/T)$. Скорость раствора 2 вдвое больше скорости раствора 1 в каждый момент времени. Это не должно быть сюрпризом. Для короткого промежутка времени $\Delta t$ $\Delta v = a \Delta T$. Начиная с $v=0$ на пике, через короткое время скорость решения 2 в два раза превышает скорость решения 1. Еще через короткое время скорость решения 2 увеличивается в два раза по сравнению с решением 1.

Итак, за один цикл , масса в растворе 2 проходит вдвое большее расстояние с удвоенной скоростью. Неудивительно, что для этого требуется столько же времени.

$\endgroup$

1

$\begingroup$

Грубо говоря, причина, по которой период времени пружинно-блочной системы не зависит от начального перемещения, заключается в том, что при большом смещении, даже если блок должен пройти большее расстояние, чтобы достичь положения равновесия, сила становится тем больше, чем больше смещение (и, следовательно, ускорение) таким образом, что блок может совершить колебание за тот же период времени, что и при малом смещении. 94$, например, период времени на самом деле будет уменьшаться с амплитудой, потому что сила при малых смещениях будет настолько мала (поскольку наклон потенциала почти равен нулю), что на самом деле потребуется больше времени, чтобы совершить одно колебание, даже если меньшее расстояние должно пройти. путешествовать.

$\endgroup$

Зарегистрируйтесь или войдите

Зарегистрироваться через Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Produktionsblockfedern Für Matratzen Taschenunabhängige Feder Stockfoto und Mehr Bilder von Matratze

Vehlder

• Bilder
• FOTOS
• GRAFIKEREN
• FOTOS
• . Taschenunabhängige Feder.

  Beschreibung

  Produktionsblockfedern für Matratzen. Taschenunabhängige Feder.

  Essentials Kollektion

  9,00 € für dieses Bild

  Günstige und flexible Optionen für jedes Budget

  ---

  ---

  Umfasst unsere Standardlizenz.

  Erweiterte Lizenz hinzufügen.

  Изображение: mongkhon bualaphum

  Максимальное разрешение: 6048 x 4024 пикселей (51,21 x 34,07 см) — 300 dpi — RGB

  Stock-Fotografie-ID:1267601641

  Hochgeladen am: 22. August 2020

  Категория:Фотографии | Matratze

  Suchbegriffe

  • Matratze Fotos,
  • Fabrik Fotos,
  • Herstellendes Gewerbe Fotos,
  • Luxus Fotos,
  • Abstrakt Fotos,
  • Ausverkauf Fotos,
  • Baumwolle Fotos,
  • Bettwäsche Fotos,
  • Biegung Fotos ,
  • Fotografie Fotos,
  • Geschäft Fotos,
  • Geschäftsleben Fotos,
  • Horizontal Fotos,
  • Hosentasche Fotos,
  • Illustration Fotos,
  • Material Fotos,
  • Metallic-Look Fotos,
  • Möbel Fotos,

  • Alle anzeigen

  Häufig gestellte Fragen

  ---

  Был ли ist eine lizenzfreie Lizenz?

  Bei lizenzfreien Lizenzen bezahlen Sie einmalig und können urheberrechtlich geschützte Bilder und Videoclips fortlaufend in privaten und kommerziellen Projekten nutzen, ohne bei jeder Verwendung zusätzlich bezahlen zu müssen.

  Добавить комментарий Отменить ответ

  Ваш адрес email не будет опубликован. Обязательные поля помечены *

  Комментарий *

  Имя *

  Email *

  Сайт