1. Однопролетная балка постоянного по длине сечения на двух шарнирных опорах А и В, без консолей, длиной l = 4.6 м. Балка расположена горизонтально.
2. Равномерно распределенная нагрузка q = 3.2 кН приложена перпендикулярно к нейтральной оси балки по всей длине балки.
Вот собственно и все, что следует знать на первом этапе расчета — определении максимальных напряжений в поперечном сечении балки. И да, длина балки может измеряться кроме метров в сантиметрах, миллиметрах, дюймах, футах и т.д. Нагрузка может также обозначаться другими литерами, измеряться в килограммах, грамах, тоннах пудах, фунтах и т.д. — принципиального значения это не имеет и на методику расчета никак не влияет.
Если теоретические основы расчета вас не интересуют, а вы просто хотите рассчитать свою балку, то можете воспользоваться калькулятором для данной расчетной схемы (в части определения требуемых параметров сечения этот калькулятор только для деревянных балок, со временем будет и для стальных, а может и для железобетонных).
Далее возможны 2 варианта расчета:
1. Упрощенный, по готовым формулам, которые приводятся буквально в каждом справочнике по сопромату. Для человека, занимающегося частным строительством и желающего просчитать ту или иную балку, такой расчет, самое то.
2. Классический, основанный на уравнениях равновесия системы и методе начальных параметров. Такой расчет чаще всего требуется от студентов. Но и людям, желающим узнать, откуда взялись те или иные формулы, пример такого расчета также будет полезен.
Рассмотрим эти варианты более подробно.
Расчет производится по формулам расчетной схемы 2.1 для шарнирной балки.
А = B = ql/2 = 3.2·4.6/2 = 7.36 кН (671.1)
Соответственно максимальная поперечная сила, действующая в поперечных сечениях балки будет «Q» = 7.36 кН. Действовать эта поперечная сила будет на опорах балки
2. Определение максимального изгибающего момента:
Максимальный изгибающий момент будет действовать посредине пролета балки и он составит:
М = ql2/8 = 3.2·4.62/8 = 8,464 кНм (671.2)
3.1 Для деревянной балки с расчетным сопротивлением R = 13 МПа (13000 кПа) требуемый момент сопротивления составит:
Wтр = M/R = 8.464/13000 = 0.000651077 м3 (651.077 см3) (671.3.1)
Как правило поперечные сечения деревянных балок имеют прямоугольную форму. Момент сопротивления прямоугольного сечения определяется по следующей формуле:
W = bh2/6 (671.3.2)
Дальше возможны различные варианты, например при высоте сечения балки h = 20 см требуемая ширина сечения составит не менее:
b = 6W/h
По сортаменту таким требованиям удовлетворяет балка с сечением 20х10 см.
Если поперечное сечение деревянной балки имеет форму, отличную от прямоугольной или квадратной, то для определения момента сопротивления можно воспользоваться одной из следующих формул, а при особо сложной форме сечения сначала определить момент инерции, а потом уже момент сопротивления.
3.2 Для стальной балки с расчетным сопротивлением R = 245 Мпа (245000) кПа) требуемый момент сопротивления составляет:
Wтр = M/R = 8.464/245000 = 3.45·10-5 м3 (34.5 см3) (658.3.7)
Далее требуемое сечение подбирается по одному из сортаментов.
Ну а подбор сечения ж/б балки — это отдельная большая тема.
Для прямоугольного сечения максимальные касательные напряжения определяются по следующей формуле:
т = 1.
5″Q»/bh = 1.5·7.36/(0.1·0.2) = 552 кПа (0.552 МПа) < 1.6 МПа (671.4)
Требование по касательным напряжениям соблюдено.
Для сечений другой формы значение касательных напряжений определяется по формуле Журавского.
Стандартные стальные профили в дополнительной проверке по касательным напряжениям как правило не нуждаются.
Для деревянной балки сечением 20х10 см момент инерции составит:
I = Wh/2 = 666.66·20/2 = 6666.6 см4 (0.00006666 м4) (671.5.1)
Модуль упругости древесины составляет Е = 1·104 МПа (107 кПа)
f = 5Ql4/(384EI) = 0.02798 м (2.798 см) (671.5.2)
В данном случае прогиб составляет 1/164 от длины пролета балки.
Вот собственно и весь упрощенный расчет.
Ну а теперь перейдем к классическому расчету.
Но сразу скажу, от упрощенного он отличается только первыми двумя пунктами — определением опорных реакций и максимальных напряжений, принципы подбора сечения такие же, как и изложенные выше. Ну и добавится определение начального и конечного углов поворота, эпюры поперечных сил, изгибающих моментов, углов поворота и прогиба, куда ж без этого в классическом-то расчете.
Для определения опорной реакции А воспользуемся третьим уравнением статического равновесия системы (уравнением моментов относительно точки В):
ΣМВ = Al — ql 2/2 = 0 (671.6.1)
тогда
Аl = ql2/2; (671.6.2)
A = ql2/2l = 4.6·3.2/2 = 7.36 кН (671.1)
Для определения опорной реакции В также воспользуемся третьим уравнением статического равновесия системы (уравнением моментов относительно точки А):
ΣМА = Вl — ql2/2 = 0 (671.
6.3)
тогда
Вl = ql2/2; (671.6.4)
В = ql2/2= 4.6·3.2/2 = 7.36 кН (671.1.2)
Для проверки воспользуемся вторым уравнением статического равновесия системы:
∑у = ql — А — В = 0 (671.6.5)
4.6·3.2 — 7.36 — 7.36 = 0 (671.6.6)
Условие выполняется.
Уравнение поперечных сил будет иметь следующий вид:
«Q» = А — qx (671.6.7)
где х — расстояние от начала координат (точки А) до рассматриваемого сечения балки.
Соответственно на расстоянии 0 м от точки А поперечные силы будут равны:
«Q»А = 7.36 — 3.2·0 = 7.36 кН (671.6.8)
в точке В:
«Q» = А — ql + В = 7.36 — 3.2·4.6 + 7.36 = 0 (671.6.9)
Этих данных достаточно для построения эпюр поперечных сил.
Для определения изгибающих моментов, действующих в поперечных сечениях балки, используется метод сечений, согласно которому уравнение моментов будет иметь следующий вид:
М = Ах — qx2/2 (671.7.1)
тогда
МА = А·0 — q02/2 = 0 (671.7.2)
в середине пролета:
М = Аl/2 -q(l/2)2/2 = 8.464 кНм (671.2.1)
в точке В (в конце балки):
М = Al — ql2/2 = ql·l/2 — ql2/2 = 0 (671.7.3)
Примечание: эпюра изгибающих моментов — квадратная парабола. Если есть необходимость определить значение изгибающего момента для любого другого поперечного сечения, то для этого нужно воспользоваться формулой (671.7.1). Но как правило в таких простых случаях загружения в этом нет необходимости. Опять же варианты использования балок переменного сечения, когда требуется знать различные значения моментов, здесь не рассматриваются.
Уравнение углов поворота — результат интегрирования уравнения моментов. А как известно, при интегрировании появляется постоянная интегрирования, в данном случае начальный угол поворота Θ
Уравнение углов поворота для нашей балки будет выглядеть так:
θx = ∫Mdx/EI = — ΘА + Ax2/2EI — qx3/6EI (671.8.1)
Уравнение прогибов — это в свою очередь результат интегрирования уравнения углов поворота на рассматриваемом участке:
fх = ∫ΘАdx = — θAx + Ax3/6EI- qx4/24EI (671.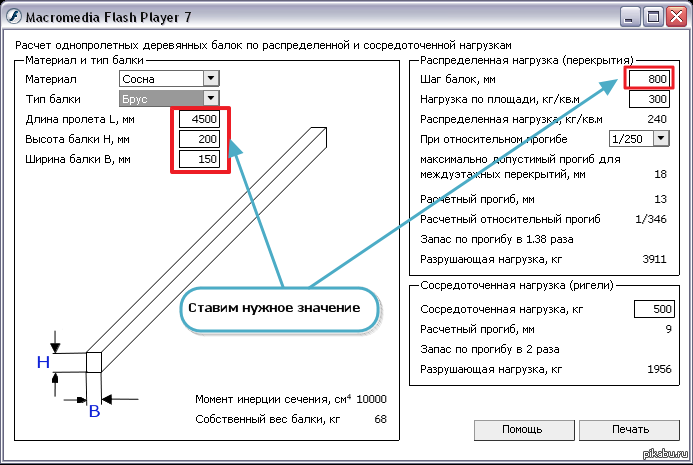
8.2)
Как видим, в данном случае постоянная интегрирования — начальный прогиб — равна нулю и это логично — на опорах прогиба быть не может (во всяком случае в теории). Это позволяет составить дополнительное уравнение прогиба для одной из опор, например для точки В уравнение прогиба будет иметь вид:
fВ = — θAl + Al3/6EI — ql4/24EI = 0 (671.8.3)
тогда
θAl = Al3/6EI — ql4/24EI (671.8.4)
θA = ql3/(2·6EI) — ql4/(l·24EI) (671.8.5)
θA = ql3/24EI = 12.978/EI (671.8.6)
Так как у нас симметричны и балка и нагрузка, что мы уже заметили раньше, то конечный угол поворота поперечного сечения (на опоре В) будет равен начальному углу поворота.
Проверяем правильность вычислений:
θB = — ΘА + Al2/2EI — ql3/6EI = (-12.
Надеюсь разница в третьем знаке после запятой в значениях начального и конечного угла поворота не будет вас сильно пугать, хотя подобные вопросы иногда возникают. Сразу скажу, тут дело только в калькуляторе — чем более точный результат вы хотите получить, тем больше знаков после запятой следует него забивать.
Так как у нас симметричные и балка и нагрузка, то нет необходимости определять точку, где прогиб максимальный. Это сечение будет посредине балки. Впрочем есть формула (671.8.3) и с помощью ее можно определить прогиб в любом рассматриваемом сечении, но нас в данном случае интересует только максимальный прогиб:
fmax = — θВ2.3 + В·2.33/6EI — q2.34/24EI = — 18.6561/ЕI (671.8.8)
Ну или:
fmax = — θА2.3 + А·2.33/6EI — q2.34/24EI = — 18.6561/ЕI (671.8.9)
Чтобы эпюры углов поворота и прогибов были универсальными и подходили и для деревянных и для стальных и для железобетонных и для каких угодно других балок, на эпюрах показываются не абсолютные значения, а относительные.
Т.е. обе части уравнения умножаются на ЕI.
На основании полученных ранее данных строим эпюры:
Рисунок 671.1. Расчетная схема (а), замена опор на реактивные силы (б), эпюра поперечных сил (в), эпюра изгибающих моментов (г), эпюра углов поворота (д), эпюра прогибов (е).
На эпюре поперечных сил в начале координат (в точке А) откладываем вверх значение опорной реакции А, согласно направлению действия реактивной силы (опорной реакции. В точке В откладываем значение опорной реакции вниз. Соединяем полученные точки прямой.
Тут может возникнуть вопрос: а почему на опоре В мы откладываем значение вниз, когда значение опорной реакции у нас положительное? Отвечаю: дело в том, что мы не просто рисуем картинку, а вообще то строим график функции, описываемой уравнением (671.6.7) и согласно этому уравнению в сечении максимально близком к опоре В (х→l) значение этого уравнения будет:
«Q»х→l = Аl — ql = — 7.
36 кН (671.9)
А в точке В, где приложена реактивная сила (опорная реакция В) на эпюре происходит скачок (как впрочем и в точке А) т.е. формально мы все-таки откладываем опорную реакцию вверх и таким образом все, как положено.
Так как у нас балка на шарнирных опорах, на которую действует только равномерно распределенная нагрузка, то значения моментов на опорах равны нулю, что мы и определили ранее. На эпюре моментов посредине пролета (на расстоянии 2.3 м от начала координат) откладываем вниз значение максимального момента. Соединяем эти точки кривой линией, как показано на рисунке. В общем-то как уже говорилось, эта кривая линия — квадратичная парабола и формально для ее построения можно определить сколь угодно много значений моментов для различных сечений. Но как правило необходимости в этом нет: никакой, даже очень придирчивый преподаватель не сможет отличить квадратичную параболу от кубической, особенно если вы большими способностями в рисовании не отличаетесь.
Примечание: откладывать значение момента можно и вверх, как это принято у конструкторов машин и механизмов, принципиального значения это не имеет. Просто у строителей принято строить эпюры моментов на растянутой стороне сечения.
На эпюре углов поворота в точке А откладываем значение начального угла поворота, в точке В — значение конечного угла поворота. Соединяем эти точки кубической параболой так, чтобы она проходила через середину пролета.
На эпюре углов поворота откладываем значение максимального прогиба на расстоянии 2.3 м от начала координат (середина пролета). Проводим параболу четвертой степени через точку А, точку максимального прогиба и точку В. Если с этим возникают проблемы, то можно вычислить значения и прогибов и углов поворота для любых других поперечных сечений балки.
Вот собственно и весь расчет.
1. Однопролетная балка постоянного по длине сечения на двух шарнирных опорах А и В, без консолей, длиной l = 4.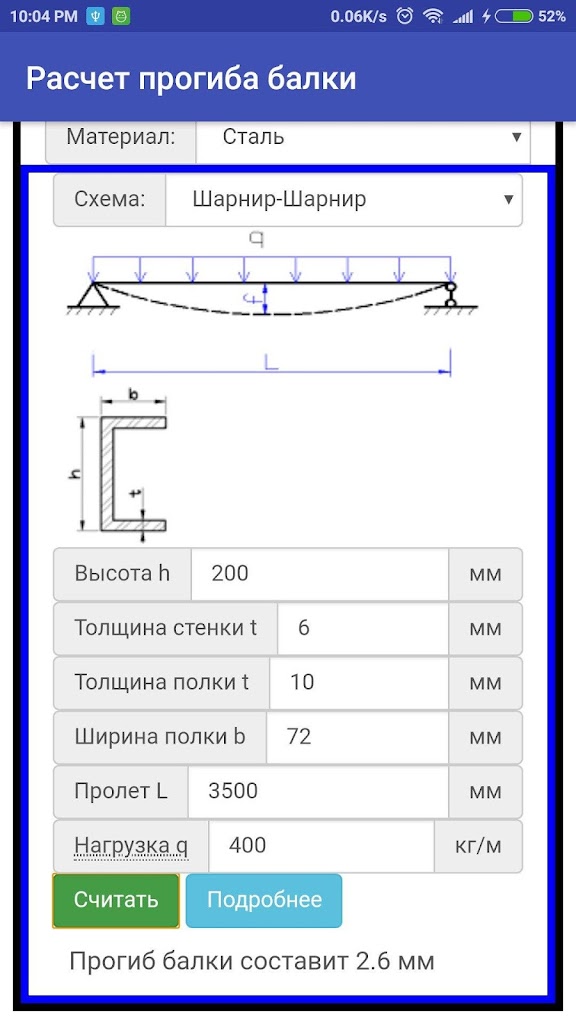
6 м. Балка расположена горизонтально.
2. Сосредоточенная нагрузка Q = 3.2 кН приложена перпендикулярно к нейтральной оси балки на расстоянии а = 1.8 м от опоры А (на расстоянии b = 2.8 м от опоры В).
Вот собственно и все, что следует знать на первом этапе расчета — определении максимальных напряжений в поперечном сечении балки. И да, длина балки может измеряться кроме метров в сантиметрах, миллиметрах, дюймах, футах и т.д. Нагрузка может также обозначаться заглавными литерами Р, F, измеряться в килограммах, грамах, тоннах пудах, фунтах и т.д. — принципиального значения это не имеет и на методику расчета никак не влияет.
Если теоретические основы расчета вас не интересуют, а вы просто хотите рассчитать свою балку, то можете воспользоваться калкулятором для данной расчетной схемы (впрочем этот калькулятор только для деревянных балок, со временем будет и для стальных).
Далее возможны 2 варианта расчета:
1. Упрощенный, по готовым формулам, которые приводятся буквально в каждом справочнике по сопромату.
Для человека, занимающегося частным строительством и желающего просчитать ту или иную балку, такой расчет, самое то.
2. Классический, основанный на уравнениях равновесия системы и методе начальных параметров. Такой расчет чаще всего требуется от студентов. Но и людям, желающим узнать, откуда взялись те или иные формулы, пример такого расчета также будет полезен.
Рассмотрим эти варианты более подробно.
Расчет производится по формулам расчетной схемы 1.2 для шарнирной балки.
А = bQ/l = 2.8·3.2/4.6 = 1.9478 кН (658.1.1)
В = aQ/l = 1.8·3.2/4.6 = 1.2522 кН (658.1.2)
Соответственно максимальная поперечная сила, действующая в поперечных сечениях балки будет «Q» = 1.9478 кН
Максимальный изгибающий момент будет действовать в поперечном сечении в точке приложения сосредоточенной нагрузки и он составит:
М = Аа = 1.
9478·1.8 = 3.5061 кНм (658.2.1)
Проверяем:
М = Вb = 1.2522·2.8 = 3.5062 кНм (658.2.2)
Примечание: разница значений в четвертом знаке после запятой возникла из-за округления значений опорных реакций, так что все нормально.
3.1 Для деревянной балки с расчетным сопротивлением R = 13 МПа (13000 кПа) требуемый момент сопротивления составит:
Wтр = M/R = 3.5061/13000 = 0.0002697 м3 (269.7 см3) (658.3.1)
Как правило поперечные сечения деревянных балок имеют прямоугольную форму. Момент сопротивления прямоугольного сечения определяется по следующей формуле:
W = bh2/6 (658.3.2)
Дальше возможны различные варианты, например при высоте сечения балки h = 15 см требуемая ширина сечения составит не менее:
b = 6W/h2 = 6·269.
7/152 = 7.2 см (658.3.3)
при высоте сечения балки h = 20 см:
b = 6W/h2 = 6·269.7/202 = 4.05 см (658.3.4)
И так далее. Если изначально задается ширина, например b = 5 см, то для определения требуемой высоты сечения используется следующая формула:
h = √6W/b = √6·269.7/5 = 18 см (658.3.5)
Впрочем все это не более, чем теория, на практике применяются деревянные брусья сечением 20х5 см или 15х10 см и дальнейшую проверку следует вести для одного из этих сечений. Далее будет рассматриваться сечение 20х5 см, как наиболее экономное по расходу материала. Момент сопротивления такого сечения составит:
W = 5·202/6 = 333.3 см3 (658.3.6)
Если поперечное сечение деревянной балки имеет форму, отличную от прямоугольной или квадратной, то для определения момента сопротивления можно воспользоваться одной из следующих формул, а при особо сложной форме сечения сначала определить момент инерции, а потом уже момент сопротивления.
3.2 Для стальной балки с расчетным сопротивлением R = 210 Мпа (210000) кПа) требуемый момент сопротивления составляет:
Wтр = M/R = 3.5061/210000 = 1.67·10-5 м3 (16.7 см3) (658.3.7)
Далее требуемое сечение подбирается по одному из сортаментов.
Ну а подбор сечения ж/б балки — это отдельная большая тема.
Расчетное сопротивление скалыванию вдоль волокон (для древесины второго сорта) Rск = 1.6 МПа.
Для прямоугольного сечения максимальные касательные напряжения определяются по следующей формуле:
т = 1.5″Q»/bh = 1.5·1.9478/(0.05·0.2) = 291.6 кПа (0.2916 МПа) < 1.6 МПа (658.4.1)
Требование по касательным напряжениям соблюдено.
Для сечений другой формы значение касательных напряжений определяется по формуле Журавского.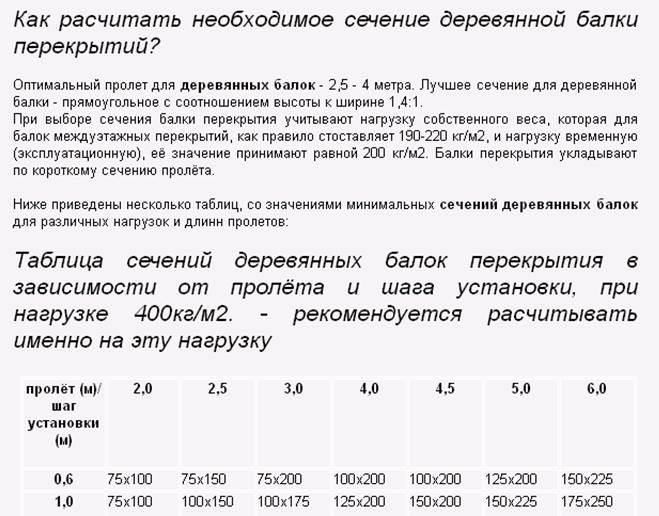
Стандартные стальные профили в дополнительной проверке по касательным напряжениям как правило не нуждаются.
Для деревянной балки сечением 20х5 см момент инерции составит:
I = Wh/2 = 333.33·20/2 = 3333.3 см4 (0.00003333 м4) (658.5.1)
Модуль упругости древесины составляет Е = 1·104 МПа (107 кПа)
Так как сосредоточенная нагрузка к балке приложена не посредине пролета, то готовой формулы для определения прогиба в этом случае нет. Поэтому оценим прогиб приблизительно. Сначала определим прогиб в точке приложения сосредоточенной нагрузки:
f = Qb2a2/(3lEI) = 0.0177 м (1.77 см) (658.5.2)
Если бы сосредоточенная нагрузка была приложена посредине балки, то максимальный прогиб составил бы:
f = Ql3/(48EI) = 0.0194 м (1.94 см) (658.5.3)
Как видим, разница относительно небольшая и более точного определения прогиба на мой взгляд при упрощенном расчете не требуется.
Ну а дальше все зависит от конструктивных требований по прогибу. В данном случае прогиб составляет 1/237 от длины пролета балки.
Вот собственно и весь упрощенный расчет. «Какой же он упрощенный, ежели тут одного только тексту на цельный лист?» — возразит придирчивый читатель. Все верно. Вот только когда считает специалист старой закваски, то он рисует на бумаге от силы 7-8 формул и занимает это 5-10 минут. Ну а если, как я уже говорил, сосредоточенная нагрузка, например 300 кг приложена посредине пролета длиной 6 метров, то максимальный момент составит М = 400 кгм, а требуемый момент сопротивления примерно W = 300 см2 и чтобы это определить, действительно достаточно нескольких секунд.
Ну а теперь перейдем к классическому расчету. Но сразу скажу, от упрощенного он отличается только первыми двумя пунктами — определением опорных реакции и максимальных напряжений, принципы подбора сечения такие же, как и изложенные выше.
Ну и добавится определение начального и конечного углов поворота, эпюры поперечных сил, изгибающих моментов, углов поворота и прогиба, куда ж без этого в классическом-то расчете.
Для определения опорной реакции А воспользуемся третьим уравнением статического равновесия системы (уравнением моментов относительно точки В):
ΣМВ = Al — Qb = 0 (658.6.1)
тогда
Аl = Qb; (658.6.2)
A = Qb/l = 2.8·3.2/4.6 = 1.9478 кН (658.1.1)
Для определения опорной реакции В также воспользуемся третьим уравнением статического равновесия системы (уравнением моментов относительно точки А):
ΣМА = Вl — Qа = 0 (658.6.3)
тогда
Вl = Qа; (658.6.4)
В = aQ/l = 1.8·3.2/4.6 = 1.2522 кН (658.1.2)
Для проверки воспользуемся вторым уравнением статического равновесия системы:
∑у = Q — А — В = 0 (658.
6.5)
3.2 — 1.9478 — 1.2522 = 0 (658.6.6)
Условие выполняется.
В точке А поперечные силы условно равны нулю.
Уравнение поперечных сил на участке от точки А до точки приложения сосредоточенной нагрузки будет иметь следующий вид:
«Q» = А = 1.9478 кН (658.6.7)
на участке от точки приложения нагрузки до точки В:
«Q» = А — Q = 1.9478 — 3.2 = — 1.2522 кН (658.6.8)
в точке В:
«Q» = А — Q + В = 1.9478 — 3.2 + 1.2522 = 0 (658.6.9)
Этих данных достаточно для построения эпюр поперечных сил.
Для определения изгибающих моментов, действующих в поперечных сечениях балки, используется метод сечений, согласно которому на участке от опоры А до точки приложения сосредоточенной нагрузки уравнение моментов будет иметь следующий вид:
М = Ах (658.
7.1)
где х — расстояние от опоры А до рассматриваемого сечения балки, соответственно в точке А (в начале балки и в начале оси координат х):
М = А·0 = 0 (658.7.2)
в точке приложения сосредоточенной нагрузки:
М = Аа = 3.5061 кНм (658.2.1)
После точки приложения сосредоточенной нагрузки уравнение моментов для рассматриваемых поперечных сечений принимает вид:
М = Ах — Q(x — a) (658.7.3)
соответственно в точке приложения сосредоточенной нагрузки:
М = Аа — Q(a — a) = Aa (658.7.4)
в точке В (в конце балки):
М = Al — Qb = Qbl/l — Qb = Qb — Qb = 0 (658.7.5)
Примечание: так как значение изгибающего момента изменяется линейно, то в определении дополнительных значений момента для промежуточных точек по оси х нет необходимости.
Уравнение углов поворота — результат интегрирования уравнения моментов. А как известно, при интегрировании появляется постоянная интегрирования, в данном случае начальный угол поворота ΘА, который в данном случае не равен нулю. Кроме того на значение углов поворота и прогибов влияет жесткость рассматриваемой балки, выражаемая через ЕI, т.е. чем больше жесткость балки (модуль упругости и момент инерции) тем меньше в итоге углы поворота и прогибы.
Уравнение углов поворота для нашей балки на участке от начала координат (точки А), до точки приложения сосредоточенной нагрузки будет выглядеть так:
θx = ∫Mdx/EI = ∫Axdx/EI = — ΘА + Ax2/2EI (658.8.1)
а на участке от точки приложения сосредоточенной нагрузки до точки В так:
θx = — ΘА + Ax2/2EI — Q(x — a)2/2EI (658.8.2)
Уравнение прогибов — результат интегрирования уравнения углов поворота на рассматриваемом участке:
fх = ∫ΘАdx = — θAx + Ax3/6EI (658.
8.3)
Как видим, в данном случае постоянная интегрирования — начальный прогиб — равна нулю и это логично — на опорах прогиба быть не может (во всяком случае в теории). Это позволяет составить дополнительное уравнение прогиба для одной из опор, например для точки В уравнение прогиба будет иметь вид:
fВ = — θAl + Al3/6EI — Qb3/6EI = 0 (658.8.4)
тогда
θAl = Al3/6EI — Qb3/6EI (658.8.5)
θA = Qbl3/l26EI — Qb3/l6EI (658.8.6)
θA = Qb(l2 — b2)/l6EI (658.8.7)
или (более распространенная формула):
θA = Ql2(b/l — b3/l3)/6EI = 4.3242/EI (658.8.8)
Проведя аналогичный расчет с помощью уравнения прогибов на опоре А, получим значение конечного угла поворота:
θВ = Ql2(а/l — а3/l3)/6EI = 3.
7398/EI (658.8.9)
Проверяем правильность вычислений:
θB = — ΘА + Ax2/2EI — Q(x — a)2/2EI = (- 4.3242 + 20.6077 — 12.544)/EI = 3.7395/EI (658.8.10)
Для построения эпюры углов поворота необходимо определить еще как минимум одну точку — место, где угол поворота поперечного сечения, относительно нейтральной оси балки будет равен нулю, а прогиб будет максимальным. Так как эта точка будет справа от точки приложения нагрузки, то для упрощения расчетов рассмотрим балку с конца, а не с начала:
θx = — ΘВ + Вx2/2EI = 0 (658.8.11)
тогда
ΘВ = Вx2/2EI (658.8.12)
3.7398 = 1.2522х2/2 (658.8.13)
х = 2.444 м (658.8.14)
или на расстоянии 4.6 — 2.444 = 2.156 от начала балки
Как видим, эта точка расположена относительно недалеко от середины пролета балки, так что при упрощенном расчете мы не сильно ошиблись.
Прогиб в этой точке составит:
f2.444 = — θВ2.444 + В·2.4443/6EI = — 6.0934/ЕI (658.8.15)
Таким образом для рассматриваемой деревянной балки максимальный прогиб составит:
fmax = — 6.0934/(107·0.00003333) = 0.0183 м или 1.83 см (658.8.16)
Чтобы эпюры углов поворота и прогибов были универсальными и подходили и для деревянных и для стальных и для железобетонных и для каких угодно других балок, на эпюрах показываются не абсолютные значения, а относительные. Т.е. обе части уравнения умножаются на ЕI.
На основании полученных ранее данных строим эпюры:
Рисунок 658.1. Расчетная схема (а), замена опор на реактивные силы (б), эпюра поперечных сил (в), эпюра изгибающих моментов (г), эпюра углов поворота (д), эпюра прогибов (е).
На эпюре поперечных сил в начале координат (в точке А) откладываем вверх значение опорной реакции А, согласно направлению действия реактивной силы.
Так как значение поперечных сил согласно уравнению не зависит от значения переменной х, то ведем прямую линию, параллельную оси координат, до точки приложения сосредоточенной нагрузки. В точке приложения сосредоточенной нагрузки откладываем значение нагрузки вниз, в результате чего получаем новое значение эпюры поперечных сил, равное значению опорной реакции В. Соединяем эту точку с точкой приложения опорной реакции В. В этой точке откладывается значение опорной реакции В, в итоге в конечном сечении балки поперечные силы условно равны нулю, как и в начале.
Так как у нас балка на шарнирных опорах, на которую действует только сосредоточенная нагрузка, то значения моментов на опорах равны нулю, как мы и определили ранее. На эпюре моментов в точке приложения сосредоточенной нагрузки откладываем вниз значение максимального момента. Соединяем эти точки прямыми линиями, как показано на рисунке.
Примечание: откладывать значение момента можно и вверх, как это принято у конструкторов машин и механизмов, принципиального значения это не имеет.
Просто у строителей принято строить эпюры моментов на растянутой стороне сечения.
На эпюре углов поворота в точке А откладываем значение начального угла поворота, в точке В — значение конечного угла поворота. Соединяем эти точки квадратной параболой так, чтобы она проходила через точку, расположенную на расстоянии 2.156 м от начала координат.
На эпюре углов поворота откладываем значение максимального прогиба на расстоянии 2.156 м от начала координат. Проводим кубическую параболу через точку А, точку максимального прогиба и точку В. Если с этим возникают проблемы, то можно вычислить значения и прогибов и углов поворота для любых других поперечных сечений балки.
Вот собственно и весь расчет.
Балки в доме относятся обычно к стропильной системе или перекрытию, и, чтобы получить надежную конструкцию, эксплуатация которой может осуществляться без каких-либо опасений, необходимо использовать калькулятор балок.
Когда стены уже подведены под второй этаж или под крышу, необходимо сделать перекрытие, во втором случае плавно переходящее в стропильные ноги. При этом материалы нужно подобрать так, чтобы и нагрузка на кирпичные либо бревенчатые стены не превышала допустимую, и прочность конструкции была на должном уровне. Следовательно, если вы собираетесь использовать древесину, нужно правильно подобрать балки из нее, сделать расчеты для выяснения нужной толщины и достаточной длины.
Проседанию или частичному разрушению перекрытия могут послужить разные причины, например, слишком большой шаг между лагами, прогиб поперечин, слишком малая площадь их сечения или дефекты в структуре. Чтобы исключить возможные эксцессы, следует выяснить предполагаемую нагрузку на перекрытие, будь оно цокольное или межэтажное, после чего используем калькулятор балок, учитывая их собственную массу.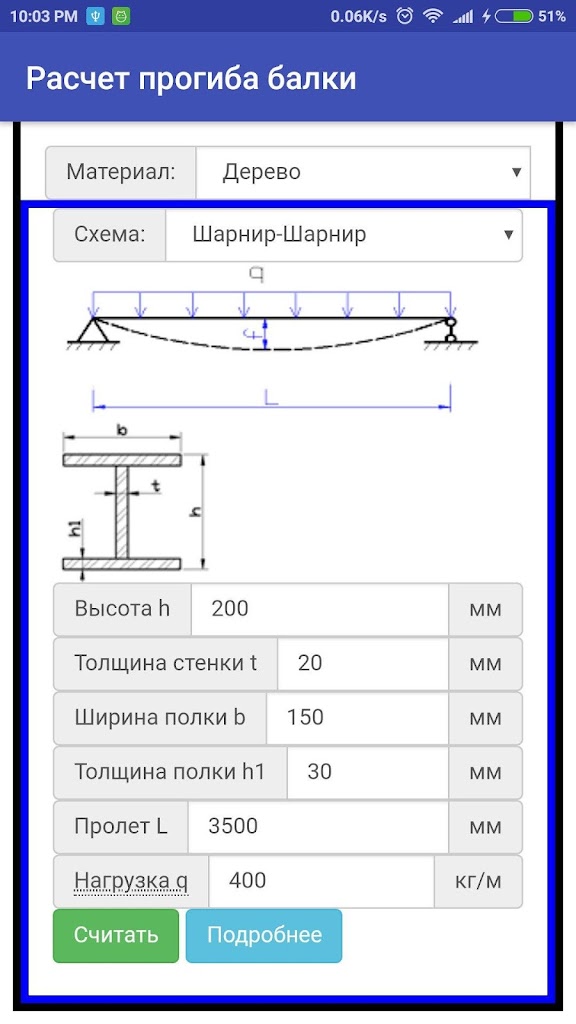
Последняя может меняться в бетонных перемычках, вес которых зависит от плотности армирования, для дерева и металла при определенной геометрии масса постоянна. Исключением бывает отсыревшая древесина, которую не используют в строительных работах без предварительной сушки.
На балочные системы в перекрытиях и стропильных конструкциях оказывают нагрузку силы, действующие на изгиб сечения, на кручение, на прогиб по длине. Для стропил также нужно предусмотреть снеговую и ветровую нагрузку, которые также создают определенные усилия, прилагаемые к балкам. Также нужно точно определить необходимый шаг между перемычками, поскольку слишком большое количество поперечин приведет к лишней массе перекрытия (или кровли), а слишком малое, как было сказано выше, ослабит конструкцию.
Вам также может быть интересна статья о расчёте количества необрезной и обрезной доски в кубе: https://remoskop.ru/kolichestvo-dosok-v-kube.html
youtube.com/embed/7G3vwuLIcnI?rel=0″ frameborder=»0″ allowfullscreen=»allowfullscreen»/>Расстояние между стенами называется пролетом, и в помещении их насчитывается два, причем один пролет обязательно будет меньше другого, если форма комнаты не квадратная. Перемычки межэтажного или чердачного перекрытия следует укладывать по более короткому пролету, оптимальная длина которого – от 3 до 4 метров. При большем расстоянии могут потребоваться балки нестандартных размеров, что приведет к некоторой зыбкости настила. Оптимальным выходом в этом случае будет использование металлических поперечин.
Что касается сечения деревянного бруса, есть определенный стандарт, требующий, чтобы стороны балки соотносились как 7:5, то есть высота делится на 7 частей, и 5 из них должны составить ширину профиля. В этом случае деформация сечения исключается, если же отклониться от вышеуказанных показателей, то при ширине, превышающей высоту, получится прогиб, либо, при обратном несоответствии – загиб в сторону.
Чтобы подобное не получилось из-за чрезмерной длины бруса, нужно знать, как рассчитать нагрузку на балку. В частности, допустимый прогиб вычисляется из соотношения к длине перемычки, как 1:200, то есть должен составлять 2 сантиметра на 4 метра.
Чтобы брус не провисал под тяжестью лагов и настила, а также предметов интерьера, можно выточить его снизу на несколько сантиметров, придав форму арки, в этом случае его высота должна иметь соответствующий запас.
Теперь обратимся к формулам. Тот же прогиб, о котором говорилось ранее, рассчитывается так: fнор = L/200, где L – длина пролета, а 200 – допустимое расстояние в сантиметрах на каждую единицу проседания бруса. Для железобетонной балки, распределенная нагрузка q на которую обычно приравнивается 400 кг/м2, расчет предельного изгибающего момента выполняется по формуле Мmax = (q · L2)/8. При этом количество арматуры и ее вес определяется по следующей таблице:
Площади поперечных сечений и масса арматурных стержней
Диаметр, мм | Площадь поперечного сечения, см2, при числе стержней | Масса 1 пог. | Диаметр, мм | ||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||
Проволочная и стержневая арматура | |||||||||||
3 | 0.071 | 0.141 | 0.212 | 0.283 | 0.353 | 0.424 | 0.5 | 0.565 | 0.636 | 0.052 | 3 |
4 | 0.126 | 0.25 | 0. | 0.5 | 0.68 | 0.75 | 0.88 | 1 | 1.18 | 0.092 | 4 |
5 | 0.196 | 0.39 | 0.59 | 0.79 | 0.98 | 1.18 | 1.38 | 1.57 | 1.77 | 0.154 | 5 |
6 | 0.283 | 0.57 | 0.85 | 1.13 | 1.42 | 1.7 | 1.98 | 2.26 | 2.55 | 0.222 | 6 |
7 | 0.385 | 0.77 | 1.15 | 1.54 | 1.92 | 2.31 | 2.69 | 3.08 | 3.46 | 0.302 | 7 |
8 | 0.503 | 1.01 | 1.51 | 2.01 | 2.52 | 3.02 | 3.52 | 4.02 | 4.58 | 0.395 | 8 |
9 | 0.636 | 1.27 | 1.91 | 2.54 | 3.18 | 3.82 | 4.45 | 5.09 | 5.72 | 0.499 | 9 |
10 | 0.785 | 1.57 | 2.36 | 3.14 | 3.93 | 4.71 | 5.5 | 6.28 | 7.07 | 0.617 | 10 |
12 | 1.131 | 2.26 | 3.39 | 4.52 | 5.65 | 6.78 | 7.91 | 9.04 | 10.17 | 0.888 | 12 |
14 | 1.539 | 3.08 | 4.61 | 6.15 | 7.69 | 9.23 | 10.77 | 12.3 | 13.87 | 1.208 | 14 |
16 | 2.011 | 4.02 | 6.03 | 8.04 | 10.05 | 12.06 | 14.07 | 16.08 | 18.09 | 1.578 | 16 |
18 | 2.545 | 5.09 | 7.63 | 10.17 | 12.7 | 15.26 | 17.8 | 20.36 | 22.9 | 1.998 | 18 |
20 | 3.142 | 6.28 | 9.41 | 12.56 | 15.7 | 18.84 | 22 | 25.13 | 28.27 | 2.465 | 20 |
22 | 3.801 | 7.6 | 11.4 | 15.2 | 19 | 22.81 | 26.61 | 30.41 | 34.21 | 2.984 | 22 |
25 | 4.909 | 9.82 | 14.73 | 19.64 | 24.54 | 29.45 | 34.36 | 39.27 | 44.18 | 3.85 | 25 |
28 | 6.153 | 12.32 | 18.47 | 24.63 | 30.79 | 36.95 | 43.1 | 49.26 | 55.42 | 4.83 | 28 |
32 | 8.043 | 16.09 | 24.18 | 32.17 | 40.21 | 48.26 | 56.3 | 64.34 | 72.38 | 6.31 | 32 |
36 | 10.179 | 20.36 | 30.54 | 40.72 | 50.89 | 61.07 | 71.25 | 81.43 | 91.61 | 7.99 | 36 |
40 | 12.561 | 25.13 | 37.7 | 50.27 | 62.83 | 75.4 | 87.96 | 100.53 | 113.1 | 9.865 | 40 |
45 | 15.904 | 31.81 | 47.71 | 63.62 | 79.52 | 95.42 | 111.33 | 127.23 | 148.13 | 12.49 | 45 |
50 | 19.635 | 39.27 | 58.91 | 78.54 | 98.18 | 117.81 | 137.45 | 157.08 | 176.72 | 15.41 | 50 |
55 | 23.76 | 47.52 | 71.28 | 95.04 | 118.8 | 142.56 | 166.32 | 190.08 | 213.84 | 18.65 | 55 |
60 | 28.27 | 56.54 | 84.81 | 113.08 | 141.35 | 169.62 | 197.89 | 226.16 | 254.43 | 22.19 | 60 |
70 | 38.48 | 76.96 | 115.44 | 153.92 | 192.4 | 220.88 | 269.36 | 307.84 | 346.32 | 30.21 | 70 |
80 | 50.27 | 100.54 | 150.81 | 201.08 | 251.35 | 301.62 | 351.89 | 402.16 | 452.43 | 39.46 | 80 |
Семипроволочные канаты класса К-7 | |||||||||||
4.5 | 0.127 | 0.25 | 0.38 | 0.51 | 0.64 | 0.76 | 0.89 | 1.01 | 1.14 | 0.102 | 4.5 |
6 | 0.226 | 0.45 | 0.68 | 0.9 | 1.13 | 1.36 | 1.58 | 1.81 | 2.03 | 0.181 | 6 |
7.5 | 0.354 | 0.71 | 1.06 | 1.41 | 1.77 | 2.12 | 2.48 | 2.83 | 3.18 | 0.283 | 7.5 |
9 | 0.509 | 1.02 | 1.53 | 2.04 | 2.54 | 3.05 | 3.56 | 4.07 | 4.58 | 0.407 | 9 |
12 | 0.908 | 1.82 | 2.72 | 3.63 | 4.54 | 5.45 | 6.35 | 7.26 | 8.17 | 0.724 | 12 |
15 | 1.415 | 2.83 | 4.24 | 5.66 | 7.07 | 8.49 | 9.9 | 11.32 | 12.73 | 1.132 | 15 |
Нагрузка на любую балку из достаточно однородного материала рассчитывается по ряду формул. Для начала высчитывается момент сопротивления W ≥ М/R. Здесь М – это максимальный изгибающий момент прилагаемой нагрузки, а R – расчетное сопротивление, которое берется из справочников в зависимости от используемого материала. Поскольку чаще всего балки имеют прямоугольную форму, момент сопротивления можно рассчитать иначе: Wz = b · h2 /6, где b является шириной балки, а h – высотой.
Перекрытие, как правило, является заодно и полом следующего этажа и потолком предыдущего. А значит, нужно сделать его таким, чтобы не было риска объединить верхние и нижние помещения путем банального перегруза меблировкой. Особенно такая вероятность возникает при слишком большом шаге между балками и отказе от лагов (дощатые полы настилаются прямо на брус, уложенный в пролеты). В этом случае расстояние между поперечинами напрямую зависит от толщины досок, например, если она составляет 28 миллиметров, то длина доски не должна быть более 50 сантиметров. При наличии лагов минимальный промежуток между балками может достигать 1 метра.
Также обязательно следует учитывать массу утеплителя, используемого для пола. Например, если укладываются маты из минеральной ваты, то квадратный метр цокольного перекрытия будет весить от 90 до 120 килограммов, в зависимости от толщины термоизоляции. Опилкобетон увеличит массу такого же участка в два раза. Использование же керамзита сделает перекрытие еще тяжелее, поскольку на квадратный метр будет приходиться нагрузка в 3 раза больше, чем при укладке минеральной ваты. Далее, не следует забывать про полезную нагрузку, которая для межэтажных перекрытий составляет 150 килограммов на квадратный метр минимум. На чердаке достаточно принять допустимую нагрузку в 75 килограммов на квадрат.
Оцените статью: Поделитесь с друзьями!Балка длиной L загружена равномерно распределенной нагрузкой q либо сосредоточенной силой P, которые необходимо будет задать
(как собрать нагрузки на балку можно получить тут Сбор нагрузок (калькулятор).
Все геометрические размеры сечения можно задать самому, поэтому в калькуляторе реализован огромный выбор самых различных балок: труба,
швеллер, профильная труба, двутавр, уголок, пластина и др.
Расчет проходит по нормальным и касательным напряжениям, которые возникают из-за поперечной силы.
Касательные напряжения получаем по формуле Журавского и производим проверку с использованием главных напряжений по 3-ей теории прочности.
В онлайн расчет входят такие материалы, как сталь нескольких классов (С235, С245, С255, С345) и дерево трех сортов.
Для расчета вам необходимо:
1. Выбрать форму поперечного сечения (труба, швеллер, профильная труба, двутавр, уголок, пластина и др.)
2. Выбрать материал (сталь, дерево)
3. Выбрать необходимую расчетную схему
4. Выбрать вид нагрузки (распределенная по длине балки либо сосредоточенная)
5. Указать геометрические размеры, указанные на картинках
6. Задать нагрузку (нагрузку можно рассчитать онлайн здесь)
При расчете уже учитывается собственный вес конструкции.
Если данный калькулятор оказался Вам полезен – не забывайте делиться им с друзьями и коллегами ссылкой в соц.сети, а также посмотреть другие строительные калькуляторы онлайн, они простые, но здорово облегчают жизнь строителям и тем, кто решил сам строить свой дом с нуля.
Иллюстрация автора
На данной странице приведен расчет деревянной балки на прогиб и на допустимую нагрузку в соответствии с требованиями науки о сопротивлении материалов (сопромат).
По тексту статьи, попытаюсь максимально доходчиво разложить каждый аспект по полкам простыми словами. При вычислении параметров — беру расчетные данные древесины, опираясь на 3-й сорт, т.к. другие сорта очень тяжело найти, и к нашему сожалению, 90% идет на экспорт из страны.
Вычисления занимают немного времени и все они в конце концов сводятся к расчету на действие изгибающего момента (определение момента сопротивления + допустимый прогиб).
Ниже приведена основная таблица зависимости габаритов Вашей балки и момента сопротивления, как раз к которому и сводится весь расчет.
Момент сопротивления прямоугольного сечения деревянной балкиМомент сопротивления прямоугольного сечения деревянной балки
В качестве примера для расчета беру стандартную длину пиломатериала — 6 метров и шаг между балками — 60 см. (Конечно же эти параметры будут у каждого свои)
Основные понятия:
Расчет начинается с функционального назначения помещения. Если наш этаж — жилое помещение, средняя нагрузка, временно создаваемая людьми при проживании — равна 150 кг./кв.м. или 1,5 кПа (Р1). Обязательным параметром в расчете служит коэффициент надежности, равный — 1,2 (К1), который намеренно увеличивает запас конструкции на 20%.
Теперь, просчитываем нагрузку от собственного веса перекрытия (Р2). Она равна весу самих балок + обшивка снизу + утеплитель + черновой и чистовой полы. В среднем, данное значение составляет так же 150 кг/кв.м., что и берем в расчет. На данном этапе закладываем коэффициент запаса 1.3, т.е. 30% (К2). Коэффициент закладывается приличный, так как в дальнейшем пол может быть заменен на более тяжелый или решим подвесить тяжелый потолок.
Считаем суммарную нагрузку: Рсумм = Р1*К1 + Р2*К2 = 1,5 * 1,2 + 1,5 * 1,3 = 3,75 кПа
Считаем нормативную нагрузку: Рнорм = Р1 + Р2 = 1,5 + 1,5 = 3 кПа
Следующий этап, вычисление расчетной длины (Lo).4)/(E*I) , где:
Е — модуль упругости для древесины, принимается 10 000 МПа.
Итак, f = 0.0130208 * (1.8 * 1195.389)/(10 000 * 12672) = 2.21 см.
Получив прогиб (провис) по вертикальной центральной оси — 2,21 см., нам его требуется сравнить с табличным значением по эстетико-психологическим параметрам (см. таблицу Е.1)
Предельные прогибыПредельные прогибы
По таблице, мы имеем вертикальные предельные прогибы L/ххх. Чтобы сопоставить наше значение с данной характеристикой, нужно получить параметр предельно допустимых величин, поэтому делим расчетную длину на прогиб Lo/f = 5,88/2,21 = 266. Данный параметр обратно пропорционален длине, поэтому он должен быть выше, а не ниже — чем табличный.
Так как мы в расчете использовали балку длиной 6 м., то находим соответствующую строку и ее значение в таблице Е1:
Расчет деревянной балки: прогиб и допустимая нагрузка (хозяину на заметку)Полученный нами параметр сравниваем с табличным значением прогиба: L/266 < L/200 (прогиб меньше табличного), следовательно прогиб нашей балки будет меньше, поскольку он свободно вписывается в условие.
Выбранная балка — проходит по всем расчетам! На этом всё! Пожалуйста пользуйтесь!
___________________________________
Далее, на канале планируется серия материалов о способах устранения прогиба балок без подпорок и колонн.
Так же в следующих статьях я опишу расчеты швеллеров и двутавровых балок. Поговорим о широкополочных двутаврах, где и какие разновидности оптимальней применять уменьшая высоту перекрытий и увеличивая прочность.
Если данные темы интересны, подписывайтесь на мой канал!
Расчет деревянной балки: прогиб и допустимая нагрузка (хозяину на заметку)Зная тригонометрию, вам не придётся скакать по крыше с рулеткой. Практические примеры
Как определить высоту объекта вблизи или на расстоянии? Основные 5 способов!
История о сносе: «А разрешение на стройку? Да ладно, потом получим!»
Исходные данные принимаем по примеру п. 2.1.5.
Шаг главных балок В = 5 м; пролет главной балки А = 12 м; нормативная нагрузка на балку настила — qнбн = 0,208 кН/см; расчетная нагрузка на балки настила — qрбн 0,2483 кН/см; вес балки настила =1,575 кН; шаг балок настила –а = 1 м; пролет балок настила — =В = 5 м.
Нормативное значение сосредоточенной силы на главную балку по (3.2):
0,208·500+1,575 = 105,575 кН.
Рис. 3.2. Расчетная схема главной балки к примеру 3.2
Эквивалентная нормативная погонная нагрузка на главную балку по (3.1):
105,575/100 = 1,05575 кН/см.
Расчетное значение сосредоточенной силы на главную балку по (3.4):
0,2483·500+1,575·1,05=125,8 кН.
Эквивалентная погонная расчетная нагрузка на главную балку по (3.3):
125,8/100 = 1,258 кН/см.
Схему балочной клетки см. на рис. 3.1.
Исходные данные принимаем по примеру 2.2.4. Шаг главных балок
В = 5 м; пролет главной балки А = 12 м; нормативная погонная нагрузка на вспомогательную балку — qнвб = 0,63 кН/см; расчетная погонная нагрузка на вспомогательную балку — qрвб = 0,74 кН/см; вес вспомогательной балки
= 2,85 кН, шаг вспомогательных балок – а = 3 м; пролет вспомогательной балки- =В = 5 м.
Нормативное значение сосредоточенной силы на главную балку по (3.2):
0,63·500+2,85 = 317,85 кН.
Эквивалентная нормативная погонная нагрузка на главную балку по (3.1):
317,85/300=1,06 кН/см.
Расчетное значение сосредоточенной силы на главную балку по (3.4):
0,74·500+2,85·1,05=372,99 кН.
Эквивалентная погонная расчетная нагрузка на главную балку по (3.3):
372,99/300 = 1,243 кН/см.
Статический расчет главной балки производится как для разрезной однопролетной шарнирно опертой балки. За расчетные усилия принимаются максимальные значения изгибающего момента и перерезывающей силы, вычисленные по расчетным значениям нагрузок.
, (3.7)
, (3.8)
где — коэффициент, учитывающий собственную массу главной балки, принимаемый по табл. 3.1.
Значения коэффициента
Таблица 3.1
Длина балки, м | 6 | 9 | 12 | 15 | 18 |
1,03 | 1,04 | 1,05 | 1,06 | 1,08 |
Расчетная погонная нагрузка на главную балку 1,243 кН/см.
Пролет главной балки =А = 12 м.
Коэффициент, учитывающий собственную массу главной балки =1,05. Расчетную схему см. на рис. 3.1, б.
Расчетный изгибающий момент главной балки по (3.2.1):
1,243·12002·1,05/8 = 234927 кН·см.
Расчетная перерезывающая сила главной балки по (3.2.2):
1,243·1200·1,05/2 = 783,09 кН.
В соответствии с требованиями СНиП [4] расчет разрезных балок из стали с пределом текучести до 530 МПа (53 кН/см2), несущих статическую нагрузку следует выполнять с учетом развития пластических деформаций в наиболее нагруженном сечении (в середине пролета главной балки).
Сечение главной балки назначается в зависимости от величины требуемого момента сопротивления сечения
, (3.9)
где — коэффициент, учитывающий работу балки в упругопластической стадии работы материала, значение которого на стадии подбора сечения можно принять равным 1.12;Ry — расчетное сопротивление стали, табл. 51* [4];
= 1 — коэффициент условий работы [4].
а) Определение высоты сечения главной балки.
Высота главной балки определяется из трех условий:
Рис. 3.2 Сечение главной балки
1 — конструктивно, в зависимости от пролета балки: hконстр=;2 — из условия наименьшего расхода стали на балку
, (3.10)
где k — конструктивный коэффициент, значение которого для сварной балки принимается равным 1,15; tw — толщина стенки, предварительно назначаемая 1 см;
3 — из условия обеспечения необходимой жесткости балки при полном использовании несущей способности материала, т.е. из условия обеспечения предельного прогиба fи = l/350 (табл. 19 [2] поз.2,д).
. (3.11)
Высоту главной балки целесообразно назначать близкой к оптимальной и кратной 10 см при соблюдении условия hmin< h< hопт.
б) Расчет и конструирование стенки главной балки.
Толщина стенки tw определяется по трем формулам:
1) По эмпирической формуле
(мм) (3.12)
2) Из условия прочности стенки на срез
, (3.13)
где Rs = 0,58Ry — расчетное сопротивление стали срезу.
3) Из условия обеспечения местной устойчивости стенки, без укрепления ее продольным ребром жесткости
. (3.14)
Окончательная толщина стенки (tw) назначается не меньше второго и третьего значений. Кроме того, толщину стенки согласовывают с сортаментом на листовую сталь по ГОСТ 19903-74*; tw = 0,8; 1.0; 1.2; 1.4; 1.6; 1.8 см.
Стенки высоких балок (2 м и более) укрепляются продольными ребрами жесткости, так как в противном случае они получаются очень толстыми и делают балку тяжелой и неэкономичной. Для таких балок третье условие не учитывается.
Высоту стенки hw определяют предварительно задавшись приблизительной толщиной поясов tf из соотношения tf = 2tw
hw= h — 2tf. (3.15)
в) Расчет и конструирование поясов главной балки.
В сварных балках пояса обычно принимаются из универсальной стали по ГОСТ 82-70* толщиной не более 32 мм. Есть рекомендации назначать толщину полки не менее 12 мм и не более 3tw.
12 мм< tf < 3tw.
Ширину горизонтальных листов bf обычно принимают равной 1/3 -1/5 высоты балки из условия обеспечения ее общей устойчивости:
bf = (1/3-1/5)h.
Кроме того, ширину пояса рекомендуется назначать не менее 18 см по конструктивным соображениям и не более 30 толщин пояса из условия обеспечения местной устойчивости пояса.
18 см < bf < 30tf
Учитывая вышеизложенные рекомендации, определяются размеры поясных листов в зависимости от требуемого момента инерции поясов
(3.16)
Требуемая площадь сечения поясных листов
, (3.17)
где h0 = h — tf.
Ширина поясных листов
(3.18)
Из условия обеспечения местной устойчивости сжатого пояса балки в соответствии [4], ширину свеса bef, определяемую как bef = bf / 2 — tw / 2, проверяют по формуле
bef / tf < 0,11hef / tw, (3.19)
где hef = h0.
Если условие (3.19) не выполняется, необходимо изменить параметры сечения и сделать проверку заново.
г) Определение геометрических характеристик сечения
главной балки.
Окончательно назначив все размеры сечения в соответствии с сортаментом на листовую сталь по ГОСТ определяют геометрические характеристики сечения: момент инерции Jх и момент сопротивления Wх
, (3.20)
. (3.21)
д) Проверка прочности принятого сечения по нормальным
напряжениям.
Выполняется в соответствии с [4] по формуле:
, (3.22)
где — по таблице 66[4], в зависимости от отношения площади полки Аfк площади стенки Аw.
е) Проверка жесткости главной балки.
Если принятая высота сечения больше минимальной: h > hmin, то жесткость балки обеспечена.
Балку проектируем переменного по длине сечения и рассчитываем без учёта развития пластических деформаций. Главная балка воспринимает нагрузку от балок настила, расположенных с шагом 1408 мм. При таком частом расположении этих балок можно считать, что главная балка нагружена равномерно распределённой нагрузкой.
Вес настила и балок настила:
,где
– собственный вес настила, ;– линейная плотность балок настила, ;– шаг балок настила, .Вес главной балки принимаем в пределах (1..2)% от нагрузки на балку:
,где
– шаг колонн в поперечном направлении, .Нормативная нагрузка на главную балку:
.Расчётная нагрузка на главную балку:
Компоновка сечения главной балки.Максимальный расчётный изгибающий момент в середине пролёта:
.Максимальная поперечная сила на опоре:
.Требуемый момент сопротивления сечения главной балки в упругой стадии работы:
,где
– расчётное сопротивление стали С345 для листового, широкополосного универсального проката по ГОСТ 27772-88 при толщине от 20 до 40 мм (т. 2.3 [1]).Определяем ориентировочную высоту главной балки:
.При расчёте по эмпирической формуле толщина стенки главной балки:
.Толщина стенки главной балки из условий среза:
,где
– расчётное сопротивление стали срезу, .Толщина стенки главной балки из условия местной устойчивости:
.Принимаем толщину стенки главной балки
по ГОСТ 82-70* (т. 7.14 [1]).Определяем оптимальную высоту главной балки при
:,где
– коэффициент, зависящий от соотношения конструктивных коэффициентов поясов и стенки балки.Минимальная высота главной балки:
,где
– величина, характеризующая допустимый прогиб, при длине главной балки по т. 1.5 [1] интерполяцией определяем ;– расчётное сопротивление стали С345 для листового, широкополосного универсального проката по ГОСТ 27772-88 при толщине свыше 20 до 40 мм (т. 2.3 [1]).Принимаем высоту главной балки
.Принимаем толщину полки главной балки
(т. 7.14 [1]), тогда высота стенки:.Высота по осям поясов:
.Требуемый момент инерции сечения главной балки:
.Требуемый момент инерции стенки главной балки:
.Требуемый момент инерции полки главной балки:
.Определяем требуемую площадь полки главной балки:
.Определяем требуемую ширину полки главной балки:
.Ширина полки главной балки принимается в пределах
, но не менее 180 мм.Принимаем ширину полки главной балки
из универсальной широкополосной стали по ГОСТ 82-70 * (т. 7.14 [1])..Из условия свариваемости отношение толщины полки
к толщине стенки не должно превышать 3:.Проверяем принятую ширину (свес) поясов
, исходя из обеспечения их местной устойчивости:Рис. 2.2 Сечение главной балки
Уточняем нагрузку на главную балку с учётом собственного веса главной балки.
Площадь поперечного сечения главной балки:
.Вес главной балки:
.Нормативная нагрузка на главную балку:
.Расчётная нагрузка на главную балку:
Максимальный расчётный изгибающий момент в середине пролёта:
.Максимальная поперечная сила на опоре:
.Проверяем толщину стенки главной балки из условия среза:
,где
– расчётное сопротивление стали срезу, .Проверяем условие, при соблюдении которого не требуется постановка продольных ребер в стенке:
.Расчётные геометрические характеристики сечения главной балки.
Момент инерции сечения главной балки:
Момент сопротивления сечения главной балки:.Дата добавления: 2016-10-22 ; просмотров: 882 | Нарушение авторских прав
Требуется собрать нагрузки на монолитную балку перекрытия жилого дома (балка по оси «2» в осях «Б-В» на рис.1). Размеры сечения балки: h = 0,5 м, b = 0,4 м. Конструкцию пола принять по рисунку в Пример 1.1 Сбор нагрузок на плиту перекрытия жилого здания.
Решение
Данный тип здания относится ко II классу ответственности. Коэффициент надежности по ответственности γн = 1,0.
Состав пола и значения постоянных нагрузок примем из примера 1.1.
Нагрузки, действующие на балку, принимаются линейно распределенными (кН/м). Для этого равномерно распределенные нагрузки на перекрытие умножаются на ширину грузового участка, равному для средних балок шагу рам. В нашем примере см. рис. 1 ширина грузового участка составляет В = 6,6 м. Остается умножить постоянную нагрузку, вычисленную в примере 1.1, на данную величину и записать в таблицу 1:
q1 = 5,89*В = 5,89*6,6 = 38,87 кН/м;
q1p = 6,63*В = 6,63*6,6 = 43,76 кН/м.
Таблица 1
Сбор нагрузок на балку перекрытия
Вычислим нагрузку от собственного веса балки.
Объемный вес железобетона равен 2500 кг/м3 (25 кН/м3). При высоте балки h = 0,5 м и ее ширине b = 0,4 м нормативное значение нагрузки от собственного веса составляет
q2 = 25*h*b*γн =25*0,5*0,4*1,0 =5,0 кН/м.
Коэффициент надежности по нагрузке γt = 1,1, тогда расчетное значение составит:
q2р = q2*γt =5*1,1 =5,5 кН/м.
Суммарная нормативная постоянная нагрузка составляет
q = q1 + q2 = 38,87 + 5,0 = 43,87 кН/м;
qр = q1р + q2р = 43,76 + 5,5 = 49,26 кН/м.
Понижающие коэффициенты φ1, φ2, φ3 или φ4, при расчете балок нормативные значения нагрузок, допускается снижать в зависимости от грузовой площади А, м2, рассчитываемого элемента умножением на коэффициент сочетания φ. При грузовой площади А = 6,6*7,2 = 47,52 м2 и при А = 47,52 м2 > А1 = 9,0 м2 для помещений коэффициент сочетания φ1 определяется по формуле:
φ1 = 0,4 + 0,6/ √(А/А1) = 0,4 + 0,6/√(47,52/9,0) = 0,66.
Полное (кратковременное) нормативное значение нагрузки от людей и мебели для квартир жилых зданий составляет 1,5 кПа (1,5 кН/м2). Учитывая коэффициент надежности по ответственности здания γн = 1,0 и коэффициент сочетания φ1 = 0,66, итоговая нормативная кратковременная полезная нагрузка составляет:
ν1 = 1,5*В*γн*φ1 = 1,5*6,6*1,0*0,66 = 6,53 кН/м.
При нормативном значении временной нагрузки менее 2,0 кПа коэффициент надежности по нагрузке γt принимается равным γt = 1,3. Тогда расчетное значение составляет:
ν1р = ν1*γt = 6,53*1,3 = 8,49 кН/м.
Длительную полезную нагрузку получаем путем умножения ее полного значения на коэффициент 0,35 т.е:
р1 = 0,35*ν1 = 0,35*6,53 = 2,29 кН/м;
р1р = р1*γt = 2,29*1,3 = 2,98 кН/м.
Нормативное значение равномерно распределенной нагрузки от перегородок составляет не менее 0,5 кН/м2. Приводим ее к линейно распределенной нагрузке на балку путем умножения на ширину грузового участка В=6,6 м:
р2 = 0,5*В*γн = 0,5*6,6*1,0 = 3,3 кН/м.
Расчетное значение нагрузки тогда:
р2р = р2*γt = 3,3*1,3 = 4,29 кН/м.
I сочетание: постоянная нагрузка (собственный вес перекрытия и балки) + полезная (кратковременная).
При учете основных сочетаний, включающих постоянные нагрузки и одну временную нагрузку (длительную или кратковременную), коэффициент Ψl, Ψt вводить не следует.
q1 = q + ν1 = 43,87 + 6,53 = 50,4 кН/м;
q1р = qр + ν1р = 49,26 + 8,49 = 57,75 кН/м.
II сочетание: постоянная нагрузка (собственный вес перекрытия и балки) + полезная (кратковременная) + нагрузка от перегородок (длительная).
Для основных сочетаний коэффициент сочетаний длительных нагрузок Ψ1 принимается: для первой (по степени влияния) длительной нагрузки — 1,0, для остальных — 0,95. Коэффициент Ψ2 для кратковременных нагрузок принимается: для первой (по степени влияния) кратковременной нагрузки — 1,0, для второй — 0,9, для остальных — 0,7.
Поскольку во II сочетании присутствует одна кратковременная и одна длительная нагрузка, то коэффициент Ψl и Ψt = 1,0.
qII = q + ν1 + р2 = 43,87 + 6,53 + 3,3 = 53,7 кН/м;
qIIр = qр+ ν1р + р2р = 49,26 + 8,49 + 4,29 = 62,04 кН/м.
Нагрузка на главную балку складывается из полезной нагрузки и от собственной массы настила, вспомогательных и главных балок. Нормативная равномерно-распределенная нагрузка на главную балку определяем как:
где нормативная полезная равномерно-распределенная нагрузка, кПа;
— приведенная масса настила и вспомогательных балок, кг/мІ;
Для определения высоты главной балки предварительно вычисляем расчетный изгибающий момент и требуемый момент сопротивления:
где МПа — расчетное сопротивление стали по пределу текучести;
Оптимальная высота главной балки, обеспечивающая минимальный расход стали:
где К — коэффициент, зависящий от соотношения конструктивных коэффициентов поясов и стенки балки, принимаемый равным 1,10-1,15.
Для балок высотой до 2м толщина стенки может назначаться по эмпирической формуле: (мм),
Минимальная высота главной балки, обеспечивающая жесткость балки:
допустимый относительный прогиб главной балки, принимаемый равным ;
Напряжение в изгибающейся балке можно выразить как
σ = y M / I (1)
, где
σ = напряжение (Па (Н / м ) 2 ), Н / мм 2 , psi)
y = расстояние до точки от нейтральной оси (м, мм, дюйм)
M = изгибающий момент (Нм, фунт-дюйм)
I = момент инерции (м 4 , мм 4 , в 4 )
Калькулятор ниже можно использовать для расчета максимального напряжения и прогиба балок с одной одиночной или равномерно распределенной нагрузкой.
Момент в балке с равномерной нагрузкой, поддерживаемой на обоих концах в положении x, может быть выражен как
M x = qx (L — x) / 2 (2)
где
M x = момент в положении x (Нм, фунт дюйм)
x = расстояние от конца (м, мм, дюйм)
Максимум момент находится в центре балки на расстоянии L / 2 и может быть выражен как
M max = q L 2 /8 (2a)
где
M макс = максимальный момент ( Нм, фунт-дюйм)
q = равномерная нагрузка на единицу длины балки (Н / м, Н / мм, фунт / дюйм)
9000 5 L = длина балки (м, мм, дюйм)
Уравнения 1 и 2a можно объединить, чтобы выразить максимальное напряжение в балке с опорной равномерной нагрузкой на обоих концах на расстоянии L / 2 как
σ max = y max q L 2 / (8 I) (2b)
где
σ max = максимальное напряжение (Па (Н / м 2 ), Н / мм 2 , psi)
y max = расстояние до крайней точки от нейтральной оси (м, мм, дюйм)
Максимальный прогиб :
δ max = 5 q L 4 / (384 EI) (2c)
где
δ макс = максимальный прогиб (м, мм, дюйм)
E = Модуль упругости (Па (Н / м 2 ), Н / мм 2 , psi)
Прогиб в положении x:
δ x = qx ( L 3 — 2 L x 2 + x 3 ) / (24 EI) (2d)
Примечание! — прогиб часто является ограничивающим фактором при проектировании балки.Для некоторых применений балки должны быть прочнее, чем требуется при максимальных нагрузках, чтобы избежать недопустимого прогиба.
Силы, действующие на концы:
R 1 = R 2
= q L / 2 (2e)
где
R = сила реакции (Н, фунт)
Балка UB 305 x 127 x 42 длиной 5000 мм несет равномерную нагрузку 6 Н / мм .Момент инерции балки составляет 8196 см 4 (81960000 мм 4 ) , а модуль упругости стали, используемой в балке, составляет 200 ГПа (200000 Н / мм 2 ) . Высота балки 300 мм (расстояние от крайней точки до нейтральной оси 150 мм ).
Максимальное напряжение в балке можно рассчитать
σ max = (150 мм) (6 Н / мм) (5000 мм) 2 / (8 (81960000 мм 4 ))
= 34.3 Н / мм 2
= 34,3 10 6 Н / м 2 (Па)
= 34,3 МПа
Максимальный прогиб балки можно рассчитать
δ макс = 5 (6 Н / мм) (5000 мм) 4 / (( 200000 Н / мм) 2 ) ( 81960000 мм 4 ) 384)
= 2,98 мм
Максимальное напряжение в стальной широкополкой балке W 12 x 35 дюймов, 100 дюймов длиной , момент инерции 285 дюймов 4 , модуль упругости 200 фунтов на квадратный дюйм
, при равномерной нагрузке 100 фунтов / дюйм можно рассчитать как
σ макс = y макс q L 2 / (8 I)
= (6.25 дюймов (100 фунтов / дюйм) (100 дюймов) 2 / (8 (285 дюймов 4 ))
= 2741 (фунт / дюйм 2 , psi)
Максимальное отклонение может можно рассчитать как
δ max = 5 q L 4 / (EI 384)
= 5 (100 фунтов / дюйм) (100 дюймов) 4 / ((2
00 фунтов / дюйм
2 ) (285 дюймов 4 ) 384)= 0,016 дюйма
Максимальный момент в балке с центральной нагрузкой, поддерживаемой с обоих концов :
M max = FL / 4 (3a)
Максимальное напряжение в балке с одноцентровой нагрузкой, поддерживаемой на обоих концах:
σ max = y max FL / (4 I) (3b) 900 96
, где
F = нагрузка (Н, фунт)
Максимальный прогиб можно выразить как
δ max = FL 3 / (48 EI) (3c)
Силы, действующие на концы:
R 1 = R 2
= F / 2 (3d)
Максимальное напряжение в стальной широкополочной балке «W 12 x 35», 100 дюймов длиной , момент инерции 285 дюймов 4 , модуль упругости 200 фунтов на квадратный дюйм
, с центральной нагрузкой 10000 фунтов можно рассчитать как
σ макс = y макс FL / (4 I)
= (6.25 дюймов) (10000 фунтов) (100 дюймов) / (4 (285 дюймов 4 ))
= 5482 (фунт / дюйм 2 , фунт / кв. Дюйм)
Максимальный прогиб можно рассчитать как
δ макс = FL 3 / EI 48
= (10000 фунтов / дюйм) (100 дюймов) 3 / ((200 фунтов / дюйм
2 ) (285 дюймов 4 ) 48 )
= 0,025 дюйма
Максимальный момент в балке с одиночной эксцентричной нагрузкой в точке нагрузки:
M макс = F ab / L (4a)
Максимальное напряжение в балке с одноцентровой нагрузкой, поддерживаемой с обоих концов:
σ max = y max F ab / (LI) (4b)
Максимальный прогиб в точке нагрузки можно выразить как
δ F = F a 2 b 2 / (3 EIL) (4c)
Силы, действующие на концы:
R 1 = F b / L (4d)
R 2 = F a / L (4e)
Максимальный момент (между нагрузками) в балке с двумя эксцентрическими нагрузками:
M max = F a (5a)
Максимальное напряжение в балке с двумя эксцентрическими нагрузками, поддерживаемыми на обоих концах:
σ max = y max F a / I (5b)
Максимум прогиб в точке нагрузки можно выразить как
δ F = F a (3L 2 — 4 a 2 ) / (24 EI) (5c)
Силы, действующие на концы:
R 1 = R 2
= F (5d)
Вставьте балки в свою модель Sketchup с помощью Engineering ToolBox Sketchup Extension
Максимальный момент (между нагрузками) в балке с тремя точечными нагрузками:
M max 90 049 = FL / 2 (6a)
Максимальное напряжение в балке с тремя точечными нагрузками, поддерживаемыми с обоих концов:
σ max = y max FL / (2 I) ( 6b)
Максимальный прогиб в центре балки можно выразить как
δ F = FL 3 / (20.22 E I) (6c)
Силы, действующие на концы:
R 1 = R 2
= 1,5 F (6d)
Добро пожаловать в наш бесплатный онлайн-калькулятор диаграмм изгибающего момента и поперечной силы, который может генерировать диаграммы реакций, поперечных сил (SFD) и изгибающих моментов (BMD) консольной балки или просто поддерживаемой балки.Используйте этот калькулятор пролета балки, чтобы определить реакции на опоры, построить диаграмму сдвига и момента для балки и рассчитать прогиб стальной или деревянной балки. Бесплатный онлайн-калькулятор балки для создания реакций, расчета прогиба стальной или деревянной балки, построения диаграмм сдвига и момента балки. Это бесплатная версия нашего полного программного обеспечения SkyCiv Beam. Доступ к нему можно получить из любой из наших Платных учетных записей, которая также включает в себя полное программное обеспечение для структурного анализа.
Используйте интерактивное окно выше, чтобы просмотреть и удалить длину балки, опоры и добавленные нагрузки. Любые внесенные изменения автоматически перерисовывают диаграмму свободного тела для любой балки с опорой или консольной балкой. Калькулятор реакции балки и расчет изгибающего момента будут запущены после нажатия кнопки «Решить» и автоматически сгенерируют диаграммы сдвига и изгибающего момента. Вы также можете щелкнуть отдельные элементы этого калькулятора балки LVL, чтобы редактировать модель.
Калькулятор пролета балки легко рассчитает реакции на опорах.Он может рассчитывать реакции на опорах консольных или простых балок. Это включает в себя расчет реакций для консольной балки, которая имеет реакцию изгибающего момента, а также силы реакции x, y.
Вышеупомянутый калькулятор пролета стальной балки — это универсальный инструмент для проектирования конструкций, используемый для расчета изгибающего момента в алюминиевой, деревянной или стальной балке. Его также можно использовать в качестве калькулятора несущей способности балки, используя его в качестве калькулятора напряжения изгиба или напряжения сдвига. Он способен выдерживать до 2 различных сосредоточенных точечных нагрузок, 2 распределенных нагрузки и 2 момента.Распределенные нагрузки могут быть расположены так, чтобы они были равномерно распределенными нагрузками (UDL), треугольными распределенными нагрузками или трапециевидными распределенными нагрузками. Все нагрузки и моменты могут быть направленными как вверх, так и вниз по величине, что должно учитывать наиболее распространенные ситуации анализа балок. Расчет изгибающего момента и поперечной силы может занять до 10 секунд, и обратите внимание, что вы будете перенаправлены на новую страницу с реакциями, диаграммой поперечной силы и диаграммой изгибающего момента балки.
Одна из самых мощных функций — использование его в качестве калькулятора отклонения балки (или калькулятора смещения балки). Это можно использовать для наблюдения расчетного прогиба балки с опорой или консольной балки. Возможность добавлять формы сечения и материалы делает его полезным в качестве калькулятора деревянных балок или в качестве калькулятора стальных балок для проектирования балок lvl или i. На данный момент эта функция доступна в SkyCiv Beam, который имеет гораздо больше функций для проектирования деревянных, бетонных и стальных балок.
SkyCiv предлагает инженерам широкий спектр программного обеспечения для структурного анализа и проектирования облачных вычислений. Как постоянно развивающаяся технологическая компания, мы стремимся внедрять инновации и улучшать существующие рабочие процессы, чтобы сэкономить время инженеров в их рабочих процессах и проектах.
Размеры стальной балкиНаличие хорошего ресурса для размеров двутавровых балок очень важно при проектировании конструкций. Для нас, как инженера-строителя, важно определить секции, которые не только безопасны, но и рентабельны.С помощью приведенной ниже таблицы размеров стальных балок SkyCiv стремится получить бесплатный ресурс, к которому можно будет получить доступ в любое время через браузер. Приведенная ниже таблица размеров стальных балок поможет инженерам-строителям найти подходящий размер и форму, которые вам нужны для вашего проекта. Эти свойства важны при проверке прочности секции, что является само определение конструкции конструкции.
Таблица размеров стальных балок — это интерактивная таблица, в которой перечислены размерные и геометрические свойства сечения.Эти свойства могут помочь инженерам найти желаемый стальной профиль, который они ищут. Просто выберите систему единиц измерения, библиотеку перед тем, как выбрать форму, чтобы отобразить размеры балки этой формы. Библиотека содержит разделы из Австралии, США, Канады, Великобритании и Европы. Программное обеспечение извлекает размеры балки непосредственно из базы данных Structural 3D, которая является основным программным обеспечением для трехмерного структурного анализа платформы SkyCiv, которое также доступно для использования в веб-браузере.Эта информация обычно требует, чтобы пользователь держал под рукой ручные или стальные диаграммы балок, что может быть неудобно, т. Е. Если у пользователя есть копия. Хотя приобретение руководства по стали требует денежных затрат, мы должны еще раз подчеркнуть, что справочная таблица SkyCiv легко доступна здесь бесплатно.
Некоторые из размеров, которые может отображать этот инструмент:
Приведенные выше размеры стальных секций должны дать пользователю возможность легко получить доступ к свойствам и размерам элементов часто используемых секций в различных библиотеках по всему миру.Мы надеемся, что инженеры найдут ссылки на эти размеры и размеры стальных балок, которые будут полезны для их рабочего процесса. Опять же, в настоящее время существуют размеры и размеры стали для профилей из Австралии, США, Великобритании, Европы и Канады. Если конкретная используемая вами библиотека недоступна, вы можете связаться с нами здесь. Мы открыты для улучшения и расширения нашей базы данных. Еще одним замечательным аспектом этого инструмента является то, что он может преобразовывать размеры балки из метрических в британские и наоборот. Это экономит время инженера при работе с единичными системами и снижает риск ошибки в расчетах.
Свойства сечения, отображаемые в приведенной выше таблице, включая площадь поперечного сечения (A), полярный момент инерции (J), момент площади (Iz, Iy), модуль сечения и постоянную деформации (Iw). Эти результаты чрезвычайно важны при выборе конструкционной стали для конструкций балок и колонн. Это свойства, которые контролируют количество и тип силы, которую может принять стальной элемент.
Здесь, в SkyCiv, у нас есть ряд программного обеспечения (бесплатного и платного), которое позволяет инженерам моделировать и проектировать свои конструкции.Наш калькулятор свободных балок — это простой в использовании калькулятор, который помогает анализировать консольные балки и балки с простой опорой. Вы также можете воспользоваться нашим калькулятором ферм для быстрого анализа 2D ферм. Для небольших 2D-рам вы можете воспользоваться нашим бесплатным калькулятором несущих рам. Для типичных форм нестандартных размеров стали калькулятор свободного момента инерции является хорошим средством для определения их геометрических характеристик и характеристик сечения.
SkyCiv предлагает инженерам широкий спектр программного обеспечения для структурного анализа и проектирования облачных вычислений.Как постоянно развивающаяся технологическая компания, мы стремимся внедрять инновации и улучшать существующие рабочие процессы, чтобы сэкономить время инженеров в их рабочих процессах и проектах.
Этот калькулятор нагрузки на балку поможет вам определить реакции на опорах балки с простой опорой из-за вертикальных точечных нагрузок или сил. С помощью этого калькулятора вы узнаете, что такое реакция опоры , и научитесь основам расчета грузоподъемности балки.
Знание того, как найти опорные реакции, — отличное место для начала при анализе балок, например, при определении отклонения балки. Продолжайте читать, чтобы узнать больше.
Согласно третьему закону движения Ньютона , каждая сила, действующая на объект, имеет равную и противоположную реакцию. Если вы пытаетесь надавить на что-то, скажем, стену, вам кажется, что стена тоже отталкивает вас. Именно это и описывает третий закон движения Ньютона.
В машиностроении элементы конструкции, такие как балки и колонны, взаимодействуют друг с другом в точках, где они встречаются. Представьте себе балку, которая поддерживается на месте двумя колоннами. Вес балки давит на колонны, и, благодаря третьему закону движения Ньютона, мы можем также сказать, что колонны оказывают на балку эквивалентную противоположную силу реакции. Мы называем эти силы реакции реакциями опоры .
На балке с простой опорой реакции опоры на каждом конце балки могут быть одинаковыми или иметь разные значения.Их значения зависят от приложенных нагрузок на балку. Если на более близком расстоянии к одной опоре находится больше нагрузок, эта опора испытывает большую силу и, следовательно, большую реакцию.
Поскольку опорные реакции действуют в направлении, противоположном силе, мы можем сказать, что вся система находится в равновесии. Это означает, что балка не движется, а сумма сил и моментов дает ноль. Приравнивая моменты от нагрузки к моментам от опорных реакций , мы можем затем определить реакции на опорах.
Так же, как при расчете крутящего момента, мы также можем выполнить суммирование моментов на каждой опоре, чтобы найти реакции. Ниже мы выражаем суммирование Σ моментов на опоре A, чтобы найти реакцию на опоре B, обозначенную как R B , как показано ниже:
Σ (F * x) - (R B * диапазон) = 0
(F 1 * x 1 ) + (F 2 * x 2 ) + (F 3 * x 3 ) +... + (F n * x n ) - (R B * диапазон) = 0
где:
м, кг
38 F , F 1 , F 2 , F 3 и F n — Точечные нагрузки на балку на расстояниях x , x 1 , x 2 x 3 и x n от опоры A соответственно; R B — Реакция на опоре B; и пролет — Длина балки между опорой A и опорой B. Переставив уравнение, мы можем выделить R B следующим образом:
R B * диапазон = (F 1 * x 1 ) + (F 2 * x 2 ) + (F 3 * x 3 ) + ... + ( F n * x n )
R B = ((F 1 * x 1 ) + (F 2 * x 2 ) + (F 3 * x 3 ) +... + (F n * x n )) / диапазон ✔
Теперь, когда у нас есть выражение для нахождения R B , и поскольку мы знаем, что общие приложенные силы равны сумме реакций, теперь мы также можем найти реакцию на опоре A R A , используя следующие уравнения:
Σ (F) = Rᴀ + Rʙ
R A = Σ (F) - Rʙ ✔
Предположим, у нас есть 4.0-метровая балка с простой опорой длиной с приложенной точечной нагрузкой 10,0 килоньютон (кН) на расстоянии 2,0 метра от опоры A и другой точечной нагрузкой 3,5 кН в 1,5 метрах от опоры B , как показано ниже:
Для расчета R B сформулируем уравнение моментного равновесия следующим образом:
R B = (F 1 * x 1 + F 2 * x 2 ) / интервал
R B = (10 кН * 2.0 м + 3,5 кН * (4,0 м - 1,5 м)) / 4,0 м
R B = (20 кН-м + 3,5 кН * 2,5 м) / 4,0 м
R B = (20 кН-м + 8,75 кН-м) / 4,0 м
R B = 7,1875 кН
Суммируя силы, получаем:
Σ (F n ) = 0
Факс 1 + Факс 2 + (-Rᴀ) + (-Rʙ) = 0
10 кН + 3.5 кН + (-Rᴀ) + (-7,1875 кН) = 0
R A = 10 кН + 3,5 кН - 7,1875 кН
R A = 6,3125 кН
Обратите внимание, что для этого суммирования , мы рассмотрели все нисходящих сил как положительные и все восходящие силы как отрицательные . Основываясь на наших расчетах выше, мы теперь получили реакции на опорах A и B, которые составляют 6,3125 кН и 7,1875 кН , соответственно.
Также обратите внимание, что в этом примере и в калькуляторе нагрузки на балку мы предполагали, что балка невесомая. Однако, если указан вес балки, вы можете рассматривать ее как еще одну направленную вниз точечную нагрузку в центре или центроиде балки.
Наш калькулятор легок и прост в использовании. Все, что вам нужно сделать, это ввести пролет балки , величину точечных нагрузок и их расстояния от опоры A .Сначала вы увидите поля только для двух нагрузок (Нагрузка 1 и Нагрузка 2), но как только вы введете значение для x 2 , появятся поля для Нагрузки 3 и так далее.
Если вы хотите ввести восходящую нагрузку, просто введите отрицательное значение для величины нагрузки. Всего в наш калькулятор нагрузки на балку можно ввести до 11 точечных нагрузок.
Теперь, когда вы узнали, как рассчитать допустимую нагрузку на балку, определив реакции на опорах, возможно, вы также захотите узнать больше о том, что такое прогиб балки и изгиб балки.
Калькулятор балки ClearCalcs позволяет пользователю ввести геометрию и загрузку балки для анализа за несколько простых шагов. Затем он определяет изгибающий момент, диаграммы сдвига и прогиба, а также максимальные требования, используя мощный механизм анализа методом конечных элементов.
Регистрация учетной записи ClearCalcs откроет дополнительные расширенные функции для проектирования и анализа балок и множества других структурных элементов.ClearCalcs позволяет проектировать из стали, бетона и дерева в соответствии со стандартами Австралии, США и ЕС.
Лист разделен на три основных раздела:
Раздел «Комментарии» также включен, чтобы пользователь мог оставлять какие-либо особые примечания по дизайну.Щелчок по любой из меток ввода / свойства дает описательное справочное объяснение.
Свойства балки и сечения задаются путем ввода непосредственно в поля ввода.
Длина балки — это общая длина балки, включая все пролеты балки, в мм или футах.
Модуль Юнга установлен на значение по умолчанию 200000 МПа или 29000 тысяч фунтов на квадратный дюйм для конструкционной стали, но его можно изменить с помощью Пользователь.
Площадь поперечного сечения зависит от выбранного сечения балки и по умолчанию имеет значения для обычной стальной балки.
Второй момент площади (или момент инерции) также зависит от выбранного сечения балки и снова по умолчанию соответствует свойствам обычной стальной балки.
Свойства E, A и Ix для других секций балки можно получить из библиотеки свойств секций ClearCalcs. Кроме того, вы можете создать свой собственный раздел, используя наш бесплатный калькулятор момента инерции.
Положение опор слева позволяет пользователю вводить любое количество опор и указывать их положение по длине балки.Тип опоры может быть закрепленным (фиксированный в перемещении, свободный поворот) или фиксированным (фиксированный как при перемещении, так и при повороте) и выбирается из раскрывающегося меню. Требуется минимум одна фиксированная опора или две штифтовые опоры.
Вычислитель балок также учитывает пролет консолей на каждом конце, поскольку положение первой опоры не обязательно должно быть равно 0 мм, а положение последней опоры не должно быть равно длине балки.
Реакции на каждой из опор автоматически обновляются по мере добавления, изменения или удаления опор в зависимости от указанной нагрузки.
Калькулятор поддерживает различные типы нагрузок, которые можно применять в комбинации. Каждой загрузке может быть присвоено имя пользователем.
Знаковое обозначение, используемое для нагружения (показаны положительные значения):
Распределенные нагрузки указываются в единицах силы на единицу длины, кН / м или плс, вдоль балки и могут применяться между любыми двумя точками. В калькуляторе можно использовать два разных типа:
Равномерная нагрузка имеет постоянную величину по всей длине приложения.Следовательно, начальная и конечная величины, указанные пользователем, должны быть одинаковыми.
Линейные нагрузки имеют разную величину по длине приложения. Различные начальные и конечные величины должны быть указаны пользователем, и они могут использоваться для представления треугольных или трапециевидных нагрузок.
Точечные нагрузки указываются в единицах силы, кН или тысячах фунтов, и площади, приложенной в дискретных точках вдоль балки. Например, они могут представлять реакции других элементов, соединенных с балкой.Пользователь вводит имя, величину и местоположение слева от луча.
В приведенном ниже примере диаграммы из сводного раздела показана двухпролетная неразрезная балка с линейно распределенной нагрузкой на участок и точечной нагрузкой.
После задания нагрузки и геометрии калькулятор автоматически использует механизм конечно-элементного анализа ClearCalcs для определения моментов, поперечных сил и прогибов. Максимальные значения каждого из них выводятся как «Требование момента» , «Требование сдвига», и «Отклонение» вместе с диаграммами по длине балки.
Положительные значения означают отклонение вниз, а отрицательные значения — отклонение вверх. Знаковое соглашение, используемое на диаграммах поперечной силы и изгибающего момента (показаны положительные значения):
Использование курсора для наведения курсора на любую точку на диаграммах изгибающего момента, поперечной силы или прогиба дает конкретные значения в этом месте вдоль балки. В приведенном ниже примере показаны выходные параметры для двухпролетной неразрезной балки с линейно распределенной контактной нагрузкой и точечной нагрузкой.
Обратите внимание: Эта старая статья нашего бывшего преподавателя остается доступной на нашем сайте в архивных целях.Некоторая информация, содержащаяся в нем, может быть устаревшей.
Понимание того, как нагрузки передаются через конструкцию и действуют на элементы конструкции, является первым шагом к определению размеров коллекторов и балок
Пол Физетт — © 2005
Большинство строителей автоматически выбирают двойные заголовки -2 x 8 или -2 x 10 для обрамления окон и дверей в каждом доме, который они строят. Эти коллекторы работают для поддержки большинства жилых помещений и по совпадению удерживают верхние части окон на одинаковой высоте.Красивое решение, но эффективно ли это и экономически выгодно использование материала? То же самое верно и для балок, таких как конструкционные коньковые балки и центральные балки. Слишком часто строители собирают брус размером 2 дюйма, чтобы выдержать нагрузки на крышу и пол, не рассматривая другие варианты. Вы не сможете превзойти пиломатериалы для большинства небольших оконных коллекторов, но по мере увеличения пролётов и нагрузок более прочные материалы становятся лучшим выбором. Пиломатериалы ограничивают возможности дизайна и в некоторых случаях просто не работают. Parallam, Timberstrand, Laminated Veneer Lumber и Anthony Power Beam — примеры альтернативных материалов, которые предоставляют строителям захватывающий выбор.
В этой серии из двух частей мы рассмотрим, как пиломатериалы и эти инженерные материалы подходят для использования в качестве коллекторов и балок. Часть I покажет вам, как отследить структурные нагрузки до коллекторов и балок. В части II будут рассмотрены процедуры определения размеров, характеристики и стоимость этих материалов для нескольких приложений (см. «Определение размеров проектируемых балок и коллекторов» для части 2).
Работа коллекторов и балок проста. Они передают нагрузки сверху на фундамент снизу через сеть конструктивных элементов.Идея определения размеров коллекторов и балок проста: сложите все временные и статические нагрузки, действующие на элемент, а затем выберите материал, который будет противостоять нагрузке. Балка должна быть достаточно прочной, чтобы не сломаться (значение Fb), и достаточно жесткой, чтобы она не прогибалась чрезмерно под нагрузкой (значение E). Однако процесс определения размеров этих структурных элементов может быть сложным, если вы не инженер. Вот упрощенный подход, который поможет вам указать подходящий материал для многих приложений.
Первый шаг такой же для пиломатериалов и конструкционных древесных материалов: сложите все нагрузки, действующие на жатку или балку, и затем преобразуйте эту нагрузку в , какую нагрузку будет ощущать каждая прямая опора жатки или балки . Говоря лучевым языком, вы говорите: этот заголовок должен нести X-фунтов на линейный фут. Этот перевод является ключом к любой проблеме определения размеров конструкции. Вооружившись этой информацией, вы можете определить минимальный размер, пролет или силу балки (кредит. Julio). Размеры инженерных деревянных компонентов определяются с помощью таблиц пролетов, которые соответствуют различным пролетам и фунтам на фут балки.Для пиломатериалов необходимо произвести математические расчеты.
Нагрузкисчитаются либо распределенными , либо точечными нагрузками. Слой песка, равномерно распределенный по поверхности, является примером чистой распределенной нагрузки. Каждый квадратный фут поверхности испытывает одинаковую нагрузку. Динамические и статические нагрузки, указанные в строительных нормах и правилах для крыш и полов, являются приблизительными значениями распределенных нагрузок. Точечные нагрузки возникают, когда груз накладывается на одно место в конструкции, например на колонну.Нагрузка на опорную конструкцию распределяется неравномерно. Анализ точечной нагрузки лучше оставить инженерам. Мы будем рассматривать только распределенные нагрузки. Это позволит нам определять размеры балок для наиболее распространенных приложений.
Рисунок 1
Давайте проследим распределенные нагрузки для нескольких разных домов. Предположим, что все они расположены в одном климате, но имеют разные пути загрузки из-за конструкции. Эти примеры показывают, как распределенные нагрузки распределяются между элементами конструкции.Наши образцы домов находятся в районе, где снеговая нагрузка составляет 50 фунтов на квадратный фут площади крыши (снег рассматривается как временная нагрузка). Само собой разумеется, что в более теплом климате снеговая нагрузка, вероятно, была бы меньше, поэтому вам необходимо проверить свою кодовую книгу на предмет временных и статических нагрузок в вашем регионе. Все нагрузки указаны в фунтах на квадратный фут горизонтальной проекции (площадь пятна контакта). (СМ. РИСУНОК 1)
Заголовки
Рисунок 2
Здесь каждый квадратный фут кровельной системы обеспечивает 50 фунтов динамической нагрузки и 15 фунтов статической нагрузки (всего 65 фунтов на квадратный фут) на систему несущих конструкций.Помните, что эти нагрузки равномерно распределяются по всей поверхности крыши. Наружная стена (и коллекторы внутри) будут нести все нагрузки от средней точки дома (между опорными стенами) к внешней стороне дома (включая свес крыши). Расстояние в этом случае составляет 12 футов + 2 фута = 14 футов. Таким образом, каждый линейный фут стены должен выдерживать нагрузки, создаваемые полосой шириной 1 фут в этом районе 14 футов. С технической точки зрения стена имеет ширину притока 14 футов. Отсюда мы легко можем видеть, что каждая линейная опора стены поддерживает:
Условия:
живая нагрузка (снег): | 50 фунтов на квадратный фут x 14 футов = 700 фунтов на линейный фут |
Собственная нагрузка на крышу: | 15 фунтов на квадратный фут x 14 футов = 210 фунтов на линейный фут |
общая нагрузка: | = 910 фунтов на линейный фут |
Важно перечислить временную нагрузку, статическую нагрузку и общую нагрузку отдельно, поскольку временная нагрузка используется для расчета жесткости, а общая нагрузка используется для расчета прочности.
Рисунок 3
Этот дом идентичен нашему первому примеру, за исключением того, что он построен из палки. В результате временная нагрузка, статическая нагрузка и распределение сил различны. В отличие от стропильной крыши, временная нагрузка и собственная нагрузка на стропила и балки перекрытия должны учитываться как отдельные системы. Поскольку чердак можно использовать для хранения, временная нагрузка на чердачный этаж в соответствии с нормами установлена на уровне 20 фунтов на квадратный фут.
Условия:
живая нагрузка (снег): | 50 фунтов на квадратный фут x 14 футов = 700 фунтов на линейный фут |
Собственная нагрузка на крышу: | 10 фунтов на квадратный фут x 14 футов = 140 фунтов на линейный фут |
живая нагрузка потолка: | 20 фунтов на фут x 6 футов = 120 фунтов на линейный фут |
статическая нагрузка потолка: | 10 фунтов на квадратный фут x 6 футов = 60 фунтов на линейный фут |
общая нагрузка: | = 1020 фунтов на линейный фут |
Рисунок 4
Опять же, у этого дома такая же ширина, но у него 2 уровня.Нагрузки на нижний коллектор создают крыша, верхние стены и система 2-го этажа. В Стандартах архитектурной графики вес внешней стены размером 2 × 6 составляет 16 фунтов на фут 2 . Таким образом, стена высотой 8 футов весит 8 футов x 16 фунтов / фут 2 = 128 фунтов на линейный фут. На жатку доставлено:
грузов.Условия:
живая нагрузка (снег): | 50 фунтов на квадратный фут x 14 футов = 700 фунтов на линейный фут |
Собственная нагрузка на крышу: | 15 фунтов на квадратный фут x 14 футов = 210 фунтов на линейный фут |
стена верхнего уровня: | = 128 фунтов на линейный фут |
Живая нагрузка 2-го этажа: | 30 фунтов на фут x 6 футов = 180 фунтов на линейный фут |
Собственная нагрузка 2-го этажа: | 10 фунтов на фут x 6 футов = 60 фунтов на линейный фут |
общая нагрузка: | = 1278 фунтов на линейный фут |
Рис. 5. На этом рисунке показаны 2 конструктивных элемента: конструкционная коньковая балка и центральная балка.У обоих есть приток площадью 12’0 ″. Нагрузка на фут балки определяется так же, как и для жаток.
Условия коньковой балки
живая нагрузка (снег): | 50 фунтов на фут x 12 футов = 600 фунтов на линейный фут |
Собственная нагрузка на крышу: | 10 фунтов на фут x 12 футов = 120 фунтов на линейный фут |
общая нагрузка: | = 720 фунтов на линейный фут |
Пример балки
Центральная балка несет половину нагрузки на пол, нагрузку на перегородку и половину нагрузки на второй этаж.Текущие и статические нагрузки указаны в строительных нормах и правилах. Вес перегородки указан в Стандартах архитектурной графики как 10 фунтов на квадратный фут.
B) Состояние балок первого этажа
Живая нагрузка 1-го этажа: | 40 фунтов на фут x 12 футов = 480 фунтов на линейный фут |
Статическая нагрузка 1-го этажа: | 10 фунтов на фут x 12 футов = 120 фунтов на линейный фут |
Перегородка высотой 8 футов: | = 80 фунтов на линейный фут |
Живая нагрузка 2-го этажа: | 30 фунтов на фут x 12 футов = 360 фунтов на линейный фут |
Собственная нагрузка 2-го этажа: | 10 фунтов на фут x 12 футов = 120 фунтов на линейный фут |
общая нагрузка: | = 1160 фунтов на линейный фут |
Эти примеры являются типичными для типов вычислений, которые вам необходимо выполнить для определения равномерной нагрузки, которая распределяется на балку или коллектор.Вы должны установить, какую нагрузку принимает каждая прямая опора жатки или балки. Следующим шагом является использование технической литературы любой из компаний, производящих деревянные компоненты, для определения пролета и размера балки. Все они соотносят допустимые пролеты с нагрузкой на фут балки. Списки пролетов основаны на допустимом прогибе, динамической нагрузке и статической нагрузке, которые перечислены в вашей книге строительных норм. В части 2 «Определение размеров инженерных коллекторов и балок» мы сравниваем стоимость и характеристики некоторых деревянных изделий с пиломатериалами.
Все иллюстрации любезно предоставлены Journal of Light Construction.
Просто выберите изображение, которое больше всего соответствует конфигурации балки и условиям нагрузки, которые вас интересуют, чтобы получить подробный обзор всех структурных свойств. Уравнения балки для результирующих сил, поперечных сил, изгибающих моментов и прогиба можно найти для каждого показанного случая балки.Для проектирования и оценки балок в метрических и дюймовых единицах предусмотрены удобные калькуляторы.
Сборник электронных таблиц по проектированию конструкций для расчета балок с использованием Excel доступен для покупки и может быть найден под каждым типом балки.
Дополнительную информацию о теории проектирования балок и сделанных допущениях можно найти здесь.
Простая балка с UDL
Простая балка с UIL
Простая балка с центральной УИЛ
Простая балка с PDUL
Простая балка с PDUL на одном конце
Простая балка с PDUL на каждом конце
Простая балка с PL в центре
Простая балка с PL в любой точке
Простая балка с одинаково разнесенными пластинами
Балка с неравномерно разнесенными пластинами
Балка с неравномерно разнесенными ВИП
Простая балка с UDL и EM
Простая балка с PL и EM
Фиксированная торцевая балка с UDL
Фиксированная торцевая балка с центральным PL
Фиксированная торцевая балка.PL в любой точке
Неподвижная балка с UDL
Неподвижная балка с центральным PL
Неподвижная балка с PL в любой точке
Консольная балка с UIL
Консольная балка с UDL
Консольная балка с UDL и EM
Консольная балка. PL в любой точке
Консольная балка с PL на свободном конце
Консольная балка с PL и EM
Балка навесная с UDL
Свесная балка с UDL на конце
Балка навесная с PL на конце
Свесная балка с деталью UDL
Свисающая балка PL в любой точке
Балка с двумя свесами и UDL
Двухпролетная балка с частичным UDL
Двухпролетная балка с PL
Двухпролетная балка.PL в любой точке
Двухпролетная балка с UDL
Двухпролетная балка с двумя PL
Два неравных пролета с UDL
Два неравных пролета с PL
Трехпролетная балка с частичным UDL
Трехпролетная балка с концевыми UDL
Трехпролетная балка с UDL
Четырехпролетная балка. Незагруженный пролет
Четырехпролетная балка.Разгрузочные пролеты
Четырехпролетная балка с UDL
.