А вы знаете, что такое годовая эффективная ставка по кредиту? Годовая эффективная ставка

Годовая эффективная ставка вознаграждения по кредиту: что это

Заключая кредитное соглашение с финансовой организацией, заемщику следует в первую очередь обратить внимание на состав и размер вознаграждения, которое он будет выплачивать. Чтобы узнать реальную стоимость займа, поможет годовая эффективная ставка вознаграждения по кредиту. Узнайте, что это такое.

Фото: Кредиты.ру

Годовая эффективная ставка вознаграждения по кредиту простыми словами

В каждом кредитном договоре, в том числе и по микрозаймам, финансовая организация указывает, какая будет годовая эффективная ставка вознаграждения. Узнайте, что такое ГЭСВ и из чего она складывается.

Годовая эффективная ставка вознаграждения — это общая сумма всех платежей, уплачиваемых заемщиком по кредитному договору. Указанная ставка вознаграждения включает в свой состав, кроме размера ежемесячных платежей, еще все взимаемые кредитным учреждением комиссии, сборы за выпуск карты, страховые платежи или плату за обслуживание счета, выдачу справок и прочее. Конкретный перечень взимаемых с клиента комиссий и платежей утвержден Постановлением Нацбанка РК от 30.05.2020 №134.

Ставка зависит от суммы кредита и срока, на который он оформлен. У каждого кредитно-финансового учреждения свой размер ГЭСВ, при этом он не должен превышать установленный лимит. Согласно Постановлению Нацбанка РК от 24.12.2020 № 377, для данного показателя установлен предел — 56%.

Читайте также: IBAN: что это такое

Годовая эффективная ставка вознаграждения: отличие от номинальной, как рассчитать

Годовая эффективная ставка отличается от номинальной тем, что учитывает все возможные расходы клиента по его кредитному договору. В то же время в кредитной (номинальной) ставке указывается лишь размер процентной ставки финансовой организации без учета других платежей по кредиту.

Фото: mikrozajm.kz

Формула расчета ГЭСВ сложна. Чтобы рассчитать показатель, воспользуйтесь специальным калькулятором. Он доступен на сайте регулятора по ссылке http://www.nationalbank.kz/?docid=1382&switch=russian.

Чтобы рассчитать величину ГЭСВ по микрокредитам (ГЭСВмк), используйте формулу, утвержденную Постановлением Нацбанка РК от 24.12.2020 №378:

ГЭСВмк = ((Св + Ск) / (Сеоз/ Сп) ) / Сп х 12 х 100

где:

Св — суммарное значение процентов по займу за весь срок договора, %;

Ск — суммарное значение комиссионных и иных платежей, связанных с обслуживанием займа, тенге;

Сеоз — суммарное значение ежемесячных остатков долгов заемщика за весь срок пользования займом, тенге;

Сп — срок погашения займа, месяцы.

Когда будете принимать решение, у какой финансовой организации лучше взять кредит, кроме процентной ставки, обращайте еще внимание на ГЭСВ. Возможно, что процент по кредиту будет небольшим, а вот комиссионные платежи сделают его совершенно невыгодным по сравнению с другими предложениями. Учитесь считать свои деньги!

Читайте также: Как перевести деньги с киви на карточку Народного банка

www.nur.kz

Годовая эффективная ставка это -

При подписании кредитного договора клиенты нередко сталкиваются с некоторыми незнакомыми терминами. Часть из них предназначена только для специалистов, имеющих определенную квалификацию, значение других следует знать каждому, кто собирается взять кредит. Во время подписания соглашения необходимо обратить внимание на наличие и значение процентной ставки. При возврате заемных средств она может заметно увеличится. При этом, не следует путать эффективную ставку по кредиту и кредитную ставку по договору. Эти две важные формулировки, несмотря на кажущееся подобие, отличаются друг от друга.

Особенности эффективной ставки вознаграждения

Условия, которые предлагаются в банке, заметно отличаются от предложений МФО, что сказывается не только на правилах оформления займов, но и на нюансах, которые связаны с переплатой, начислением процентов и другими выплатами.

Таким «подводным камнем» в этом виде бизнеса считается годовая эффективная ставка вознаграждения (ГЭСВ), которая является суммой всех расходов заемщика, и которая связана с различными выплатами финансовой организации.

Следует отметить, что эти цифры нельзя считать номинальной ставкой вознаграждения(НСВ), которая может не включать в себя все средства, выплачиваемые финансовому органу.

Чем отличается эффективная ставка от номинальной

Следует подробнее разобраться с этим сложным вопросом и выяснить, чем являются годовая эффективная ставка вознаграждения и что вызывает путаницу с терминами НСВ и ГЭСВ. Процентная ставка по кредиту определяется суммой, которую клиент должен заплатить в счет использования денежных средств за один месяц, или за один год. Но заемщик вынужден выплачивать не только проценты, но и вносить деньги за открытие и обслуживание счета, рассмотрение некоторых документов и т. д. Может присутствовать требование оплаты одноразовых комиссий и различных страховок, которые могут исказить размер действительной ставки вознаграждения и ввести клиентов в заблуждение. ГЭСВ позволяет рассматривать все достоверные показатели и учитывать абсолютно все выплаты. Также она дает возможность оценивать предложения разных банков.

Номинальная ставка может определяться только фактической стоимостью кредитов, хотя и имеет различные составляющие. В нее обязательно входит частота выплат, совершенных заемщикам, их размеры и количество. Она также состоит из всех комиссий и других подобных платежей, которые удерживались кредитором в счет оплаты дополнительных услуг, таких как выдача и обслуживание займа.

Нередко такие требования предъявляются банками, где сроки выплаты долга очень большие, поэтому, компании стараются перестраховаться с помощью добавления ряда услуг, которые влекут за собой определенные расходы.

В основном речь идет о выпуске и обслуживании карточек, страховках и т. д. МФО работают несколько иначе. Они одалживают средства на более короткий срок, и этот момент обязательно нужно учитывать, сравнивая эти организации.

Как рассчитывается эффективная ставка

В договоре указывается номинальная ставка вознаграждения, с помощью которой выражается стоимость кредита, и которая отражается на ежемесячные выплаты по нему. Рассчитывать ее следует в соответствии с правилами, утвержденными Правлением Нацбанка РК в постановлении №173. Произвести такие вычисления самостоятельно, без помощи квалифицированного специалиста, клиенту будет совсем непросто, так как для этого требуется уметь применять сложные математические формулы. Для таких операций обычно используют специальный набор компьютерных программ.

На официальном интернет-портале Национального банка Казахстана существует раздел, который посвящен помощи потребителям, имеющим намерение получить определенные финансовые услуги, где можно найти специальный калькулятор. С помощью такого электронного помощника, заемщику будет легче узнать ГЭСВ.

Большинство онлайн-ресурсов финансовых и кредитных организаций второго уровня имеют на своих страницах сервисы, позволяющие произвести расчеты практически любых платежей: ежемесячные выплаты, дополнительные начисления, оплата за обслуживание и другие. Нацбанк РК постановлением №377, от декабря 2012 года, определил предельную ставку. Этот показатель касается микрокредитов, займов в банках и некоторых других финансовых операций. Он равняется 56 %.

Ставки в разных МФО

Хотя в финансовых компаниях второго уровня ГЭСВ учитывается в обязательном порядке, оценивать выгоду различных банковских программ только по этому параметру не стоит.

Один договор может иметь намного меньшую сумму чем второй, но учитывая ряд других параметров, первый вариант может оказаться более выгодным. Чтобы выяснить, какая финансовая компания предоставляет лучшие условия займа, необходимо сравнить различные предложения по аналогичным программам, при этом, средства в них должны предоставляться на такой же срок, и их суммы должны быть одинаковыми. Только такое рассмотрение ГЭСВ может считаться объективным и всесторонним, и оно действительно помогает выбрать МФО или банк с более привлекательными предложениями.

Чтобы повысить свою финансовую грамотность, не обязательно оканчивать какое-либо учебное заведение или курсы, но знать, в чем отличия процентов от ставки ОЗ, что такое договор, и на что следует обращать внимание при заключении соглашения в первую очередь – необходимо каждому современному человеку.

Эти знания позволяют сэкономить немало времени, сил и средств.

www.mikrozajm.kz

4.2.6. Эффективная годовая процентная ставка

Различные виды финансовых контрактов могут предусматри­вать различные схемы начисления процентов. Как правило, в этих контрактах оговаривается номинальная процентная ставка, обычно годовая. Эта ставка, во-первых, не отражает реальной эффективности сделки и, во-вторых, не может быть использована для сопоставлений. Для обеспечения сравнительного анализа эф­фективности таких контрактов необходимо выбрать некий пока­затель, который был бы универсальным для любой схемы начис­ления. Таким показателем является эффективная годовая про­центная ставка r e , обеспечивающая переход от P к F n при заданных значениях этих показателей и однократном начислении процентов.

Общая постановка задачи может быть сформулирована сле­дующим образом. Задана исходная сумма Р, годовая процентная ставка (номинальная) r, число начислений сложных процентов m . Этому набору исходных величин в рамках одного года соответствует вполне определенное значение наращенной ве­личины F 1. Требуется найти такую годовую ставку re, которая обеспечила бы точно такое же наращение, как и исходная схема, но при однократном начислении процентов, т.е. m = 1. Иными словами, схемы {Р , F1 , r , m > 1} и { Р, F1 , re , m = 1} должны быть равносильными.

Из формулы (4.7) следует, что в рамках одного года:

F 1 = P · (1 + r/m)m .

Согласно определению эффективной годовой процентной ставки:

F1 =P + P · re = P · ( 1 + re)

отсюда:

re = (1 + r/m)m – 1. (4.13)

Из формулы (4.13) следует, что эффективная ставка зависит от количества внутригодовых начислений, причем с ростом m она увеличивается. Кроме того, для каждой номинальной ставки можно найти соответствующую ей эффективную ставку; две эти ставки совпадают лишь при m = 1. Именно ставка re является критерием эффективности финансовой сделки и может быть ис­пользована для пространственно-временных сопоставлений.

Пример

Предприниматель может получить ссуду а) либо на условиях ежеквартального начисления процентов из расчета 75 % годовых, б) либо на условиях полугодового начисления процентов из расчета 80 % годовых. Какой вариант более предпочтителен?

Относительные расходы предпринимателя по обслуживанию ссуды могут быть определены с помощью расчета эффективной годовой процентной ставки — чем она выше, тем больше уровень расходов. По формуле (4.13):

вариант (а) r e = (1 + 0.75/4)4 — 1 = 0,99,

вариант (б) r e = (1 + 0,80/2)2 — 1 = 0,96.

Таким образом, вариант (б) является более предпочтитель­ным для предпринимателя. Необходимо отметить, что принятие решения не зависит от величины кредита, поскольку критерием является относительный показатель — эффективная ставка, а она, как следует из формулы (4.13), зависит лишь от номиналь­ной ставки и количества начислений.

Понимание роли эффективной процентной ставки чрезвычай­но важно для финансового менеджера, поскольку принятие реше­ния о привлечении средств, например, банковской ссуды на тех или иных условиях, делается чаще всего исходя из приемлемости предлагаемой процентной ставки, которая в этом случае харак­теризует относительные расходы заемщика. В рекламных проспе­ктах непроизвольно или умышленно внимание на природе ставки обычно не акцентируется, хотя в подавляющем числе случаев речь идет о номинальной ставке, которая может весьма сущест­венно отличаться от эффективной ставки. Рассмотрим простей­ший пример.

Пример

Рассчитать эффективную годовую процентную ставку при различной частоте начисления процентов, если номинальная ставка равна 10%. По формуле (4.13):

Различие между двумя ставками может быть гораздо более разительным при заключении некоторых специальных кредитных договоров, например, при оформлении кредита на условиях до­бавленного процента.

studfiles.net

Эффективная годовая процентная ставка.

Различные виды финансовых контрактов могут предусматривать различные схемы начисления процентов. Как правило, в этих контрактах обычно оговаривается номинальная процентная ставка, которая не принимает во внимание изменение стоимости денег в связи с инфляцией.

Номинальная процентная ставка имеет следующие недостатки:

1) она не отражает реальной эффективности сделки;

2) в связи с этим она не может быть использована для сопоставления эффективности различных инвестиционных проектов.

Поэтому, для обеспечения сравнительного анализа эффективности таких контрактов применяется другой показатель, который является универсальным для любой схемы начисления процентов.

Таким показателем является эффективная годовая процентная ставка 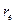, которая обеспечивает переход от PV к FV при заданной годовой процентной ставке и однократным начислением процентов.

Общая постановка задачи формулируется следующим образом.

Задана исходная сумма PV, номинальная процентная ставка r и количество начислений сложных процентов m.

Естественно, что этому набору исходных величин в рамках одного года соответствует вполне определенное значение будущей стоимости FV.

Требуется найти такую годовую ставку 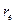, которая обеспечила бы точно такое же наращение, как и исходная схема, но при m = 1. Т.е. обе схемы должны быть равносильными.

В рамках одного года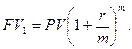

Из определения годовой эффективной ставки вытекает, что:

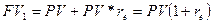, откуда .

Разделив обе части равенства на PV получим:

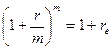. Откуда .

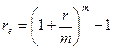Из полученной формулы видно, что эффективная ставка зависит от количества внутригодовых начислений, причем с ростом m она увеличивается. Кроме того, для каждой номинальной ставки можно найти соответствующую ей эффективную ставку. Эти две ставки совпадают при m = 1. Именно годовая эффективная процентная ставка является критерием эффективности финансовых операций и может быть использована для пространственно-временных сопоставлений.

Пример.

Предприниматель может получить ссуду на следующих условиях:

а) либо исходя из ежемесячного начисления процентов по номинальной процентной ставке 26% годовых;

б) либо исходя из полугодового начисления из расчета 27% годовых.

Какой вариант предпочтительнее?

а)

б)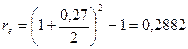

Так как эффективная годовая процентная ставка характеризует относительные расходы предпринимателя по обслуживанию ссуды, то вариант б) для предпринимателя более предпочтителен. Необходимо также отметить, что принятие решения не зависит от величины кредита, поскольку критерием является относительный показатель – эффективная процентная ставка.

Понимание роли эффективной процентной ставки чрезвычайно важно для финансового менеджера. Дело в том, что принятие решения о привлечении средств, например банковской ссуды на тех или иных условиях, делается чаще всего исходя из приемлемости предполагаемой процентной ставки, которая в этом случае характеризует относительные расходы заемщика. В рекламных проспектах непроизвольно или умышленно внимание на природе ставки обычно не акцентируется, хотя в подавляющем числе случаев речь идет о номинальной ставке, которая может весьма существенно отличаться от эффективной ставки.

Пример.

Рассчитать эффективную годовую процентную ставку при различной частоте начисления процентов, если номинальная ставка равна 10%.

M
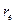	0,10	0,1025	0,10381	0,10471	0,10516

Различие между двумя ставками может быть гораздо более может быть гораздо более разительным при заключении некоторых специальных кредитных договоров, например, при оформлении кредита на условиях добавленного процента.

В финансовых соглашениях не имеет значения, какую из ставок указывать – эффективную или номинальную, поскольку использование как одной, так и другой дает одну и ту же наращенную сумму. В США в практических расчетах применяют номинальную ставку. В европейских странах, как правило, вначале определяется эффективная ставка, а затем используется формула .

Если в контракте указаны эффективная ставка и количество начислений сложных процентов, а необходимо найти номинальную ставку, то используется формула:

.

Пример.

Определить номинальную ставку, если эффективная ставка равна 18% и сложные проценты начисляются ежемесячно.

.

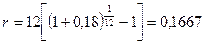Таким образом, ежегодное начисление сложных процентов по ставке 18% годовых дает какой же результат, что и ежемесячное начисление сложных процентов по ставке 16,67%.

Если две номинальные годовые процентные ставки определяют одну и ту же эффективную ставку, то они называются эквивалентными.

Пример.

Каковы будут эквивалентные номинальные годовые процентные ставки с начислениями по полугодиям и ежеквартально, если соответствующая им эффективная ставка равна 20%?

для полугодового начисления ;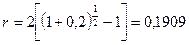

для ежеквартального начисления .

Таким образом, номинальные ставки 19,09% и 18,65% являются эквивалентными.

Мы рассмотрели наиболее стандартный и широко распространенный подход к понятию эффективной ставки.

Однако, возможны и другие подходы, которые вытекают из разнообразия финансовых соглашений. Например, вполне реальна ситуация, когда условия начисления процентов меняются: в частности, после схемы сложных процентов начиная с какого то момента времени начинают использовать схему простых процентов без прерывания действия контракта. Для анализа таких ситуаций может быть предложен следующий подход к нахождению эффективной процентной ставки. Пусть известна первоначальная сумма PV и наращенная каким либо образом за время n сумма FV. Тогда по определению:

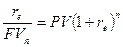и поэтому .

Пример.

В долг на 2,5 года предоставлена сумма в 30 тыс. грн. с условием возврата 40 тыс. грн. Найти эффективную ставку в этой финансовой сделке.

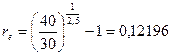или 12,196%.

Проверим полученный результат. Предположим в банк помещен вклад в размере 30 тыс. грн. на 2,5 года под 12,196% годовых сложных процентов. Тогда наращенная сумма будет равна:

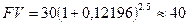тыс. грн.

Как и в случае процентной ставки можно также определить эффективную годовую учетную ставку 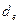. Она обеспечивает переход от к при заданных значениях этих параметров и однократном дисконтировании в течение года.

Поскольку согласно определению в рамках одного года

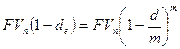, то после соответствующих преобразований получим: .

Из приведенной формулы следует, что с ростом количества начислений величина годовой учетной ставки уменьшается.

Зная годовую учетную ставку можно определить коэффициент дисконтирования: .

Используя 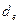можно определить эквивалентные номинальные учетные ставки.

Эффективную годовую учетную ставку можно определить иначе, если известна величина , и дисконтированная каким-либо образом за время сумма .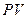

В этом случае , откуда .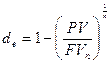

Пример.

Долговое обязательство равное 5 тыс. грн. со сроком погашения 4 года было сразу же учтено в банке и владелец обязательства получил 4,2 тыс. грн.

Найти эффективную годовую учетную ставку.

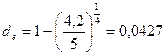
Тема 4

infopedia.su

А вы знаете, что такое годовая эффективная ставка по кредиту?

Подписывая кредитный договор, человек сталкивается со многими непонятными терминами. Оказывается, в кредитном договоре может быть указана одна процентная ставка, а когда приходится рассчитываться за кредит процентная ставка значительно выше. Существует такое понятие, как кредитная ставка по кредитному договору и эффективная кредитная ставка по кредиту. Эти две величины обозначают разные цифры и могут существенно отличатся.

Процентная ставка по кредиту это процент от суммы кредита, который заемщик будет переплачивать за пользование банковскими деньгами ежемесячно или ежегодно. Но заемщик переплачивает не только проценты по кредиту, он платит за обслуживание кредитного счета, за открытие этого счета, разные одноразовые комиссии, разные страховки, скрытые платежи и другие уплаты. В итоге стоимость кредита получается выше, чем тело кредита плюс проценты за пользование кредитом, насчитанные на весь период кредитования. Указание одной процентной ставки в договоре, и существование отличительной от нее эффективной реальной ставки вызывало возмущение со стороны потребителей. Ведь им изначально было неясно, какая реальная переплата по кредиту. Поэтому, вышел закон, который обязывает банкиров сообщать заемщику эффективную процентную ставку до совершения сделки.

Эффективная процентная ставка по кредиту или полная стоимость кредита включает в себя годовую ставку по кредиту, скрытые платежи, дополнительные комиссии, страховки и одноразовые взносы за обслуживание или открытие счета, разделенные на период оформления кредита. Таким образом, эффективная ставка по кредиту на 10 тысяч сроком на один год будет выше, чем эффективная ставка по кредиту на эту же сумму на пять лет. При этом переплата по кредиту сроком на один год будет значительно ниже, нежели переплата по кредиту сроком на пять лет.

Простая формула расчета годовой эффективной ставки выглядит следующим образом:

ЭПС = ЗС + ЕК * 12 + (ОК + 100% × (ССП + ССОП) / СК) / СрК

Аббревиатура:

ЭПС - реальная годовая ставка.

ЗС - заявленная ставка в кредитном предложении, в процентах.

ЕК - ежемесячная комиссия (за снятие средств или за пользование кредитными средствами), в процентах.

ОК - одноразовая комиссия (чаще всего применяется при выдаче полной суммы кредита), в процентах.

ССП - сумма всех страховых платежей, в денежном выражении.

ССОП - сумма сопутствующих одноразовых платежей (оформление бумаг, РКО, открытие счета, нотариальные услуги и так далее), в денежном выражении.

СК - сумма кредита.

СрК - срок погашения задолженности, в годах.

Несмотря на то, что банкиры сегодня вынуждены называть эффективную процентную ставку по кредиту, сравнивать кредитные программы только по величине эффективной ставки не следует. Эффективная кредитная ставка по кредиту зависит от сроков кредитования и суммы кредита. По одному кредитному договору эффективная ставка будет выше, чем по второму, но выгоднее может быть второй кредитный договор. Чтобы понять в каком банке предоставляют кредит на более выгодных условиях, необходимо сравнивать аналогические кредитные программы. Обе кредитные программы должны быть рассчитаны на одну саму и на такой же срок. Только тогда можно смотреть на эффективную процентную ставку и выбирать тот кредит наличными онлайн, где она получается ниже.

frombanks.ru

Временная стоимость денег - zpv_sib

Эффективная годовая процентная ставка (The Effective Annual Rate)

Годовая процентная ставка – это заявленная ставка, под которой понимается то , что проценты будут выплачены 1 раз в год. Однако на практике часто встречаются условия с выплатой сложных процентов – например, проценты выплачиваются ежеквартально, ежемесячно, ежедневно или вообще непрерывно, при этом проценты. Для того чтобы сравнивать процентные ставки по различным инструментам, с учётом различий в периодах начисления процентов, необходимо приводить все ставки к единой базе. Эффективная годовая доходность отражает фактический уровень доходности, с учётом всех периодов выплаты процентов внутри одного года. Эффективная годовая процентная ставка (EAR) рассчитывается по формуле:

 Эффективная годовая процентная ставка (EAR) = (1 + процентная ставка периода) m - 1,%

где : m = количество периодов начисления процентов        процентная ставка периода = заявленная ставка / m

Например:

Заявленная годовая ставка 9%, проценты начисляются ежемесячно методом сложного процента, тогда эффективная годовая ставка будет:

EAR = (1 + (0,09/12)) 12 - 1 = (1,0075) 12 - 1 = (1,093807) - 1 = 0,093807 или 9,38%

Понятно, что чем больше периодов начисления процентов тем больше будет EAR, и если m>1 то эффективная ставка всегда выше заявленной.

Решение кейсов на базе временной стоимости денег.

Введём понятия PV (presnt value) и FV (future value) нынешняя стоимость и будущая стоимость денег. Если задана годовая ставка, и имеются данные о периодах начисления процентов, то определить будущую стоимость можно поделив годовую ставку на количество периодов начисления процентов в году и возвести в степень равную количеству периодов умноженному на количество лет.

Например:

Необходимо определить будущую стоимость $10 000 при ставке в 8% годовых через 5 лет, с периодом начисления раз в месяц. Ставка для расчёта по формуле будет r=8/12 = 0.0067%, а количество периодов N = 12* 5 = 60.

FV = PV * (1 + 0.0067) 60 = $14 928

Обязательно перед решением подобных кейсов приводите периоды начисления N и процентную ставку r в к единым измерениям!

Текущая стоимость перпетуитета (бесконечного потока платежей).

Перпетуитет начинается как обычный аннуитет (первый денежный поток является единственным и начинается с текущего момента), но не имеет конца и продолжается бесконечно,- одним и тем же платежом последовательно в каждом периоде. Казалось бы какой смысл? Какая организация обяжет себя платить бесконечно? Однако некоторые ценные бумаги, например привелигированные акции, выпускаются в предположении что предприятие будет работать вечно, а значит и вечно выплачивать фиксированный платёж. Формула текущей стоимости бесконечного потока платежей является отправной точкой для оценки такого рода бумаг.

Упрощённо можно рассчитать так:

PV перпетуитета = аннуитетный платёж (А)                                   годовую процентную ставку (r)

Например:

Бесконечный перпетуитет $1000 при ставке в 8% , текущая стоимость такого перпетуитета будет равна 1000/0,08 = $12 500

Упрощения и допущения: N – Стремится в бесконечность, ставка положительна.

         (1) FV = PV * (1 + r)N

          (2) PV = FV *      {      1     }                                       (1 + r)Nгде: FV = будущая стоимость, PV = текущая стоимость, R = годовая процентная ставка, and N = количество лет.

Поупражняемся:

Если я открываю депозит $5000 на 5 лет с ежегодным начислением процентов, по ставке 12%, то на пятый год я получаю: 5000 * (1,12) в 5 степени = $8811,7

Или наоборот, хочу 1 000 000 через 20 лет, сколько нужно положить на депозит сейчас при ставке в 6% годовых, 1 00 000 * [1/(1,06) в степени 20] = 311 800  , т.е. сегодняшняя стоимость 1 млн долларов через 20 лет при ставке 6% составляет 311 800.

zpv-sib.livejournal.com

3. Эффективная годовая процентная ставка

Начисление процентов или доходов по разным инвестиционным проектам происходит с использованием различных схем.

Чтобы учесть частоту начисления процентов, процентную ставку и сравнить разные схемы между собой по доходности рассчитывают показатель эффективной годовой процентной ставки.

Эта ставка показывает эффективность вложений, измеренную в процентах, полученных реально за год.

,

где m — частота начислений процентов за год.

Сравнивая этот показатель по различным проектам, выделяют наиболее выгодный из них.

Пример 2 (условие в примере 1)

1. ЭГПС = =0,215

2. ЭГПС = =0,2

4. Ставка дисконта

Ставка дисконта (СД) — это коэффициент, используемый для операций дисконтирования, позволяющий учесть изменение стоимости денег во времени по отношению от будущего момента к настоящему (СД = Норма дисконта).

Ставку дисконта устанавливают для каждого инвестиционного проекта отдельно перед началом анализа эффективности данного проекта.

От устанавливаемой ставки дисконта во многом зависят выводы по эффективности проекта. Чем выше ставка дисконта, тем ниже настоящая стоимость, хуже результаты проекта.

Поэтому установление наиболее реальной, объективной ставки дисконта является очень важным моментом при оценке инвестиционного проекта.

Ставка дисконта должна удовлетворять всех участников инвестиционного проекта.

Ставку дисконта устанавливают исходя из:

1. процентной ставки;

2. минимального уровня рентабельности;

3. цены привлекаемого капитала.

1. Установление ставки дисконта на уровне процентной ставки банка по депозитным вкладам возможно только в случае стабиль функционирующей экономики страны. В этом случае процентная ставка обычно учитывает уровень инфляции и определенный уровнеь доходности, с чем и связана временная ценность денег.

2. При высоких темпах инфляции и неравномерных индексах инфляции в течение одного года процентную ставку в качестве базы для ставки дисконта использовать нельзя, т.к. она обычно не учитывает уровень инфляции.

Поэтому используют следующий поход: ставка дисконта формируется из 3-х составляющих (с учетом теории временной ценности денег):

СД = i + p + r,

где i — коэффициент, учитывающий уровень инфляции;

p — минимальный уровень рентабельности;

r — коэффициент, учитывающий степень риска.

Под минимальным уровнем рентабельности понимают гарантированный уровень получения доходов. Обычно придерживаются мнения, что наиболее гарантированными доходами являются доходы от облигаций государственного займа. В мировой практике реальный доход по ним составляет 4-5% годовых.

В качестве минимального уровня рентабельности может приниматься желаемый уровень рентабельности по данному инвестиционному проекту, а в качестве желаемого уровня рентабельности принимают процентную ставку банка.

Коэффициент, учитывающий степень риска, обычно оценивается квалифицированными экспертами, либо используются специальные методы учета степени риска при оценке инвестиционного проекта.

3. Под ценой привлекаемого капитала понимают общую сумму средств, которую необходимо уплатить за использование определенного объема финансовых ресурсов, выраженную в процентах к этому объему финансовых ресурсов.

В качестве финансовых ресурсов могут выступать собственные или заемные средства.

При использовании собственных средств в качестве цены капитала может выступать сумма дивидендов, уплаченных учредителям.

При использовании заемных средств — сумма процентов, уплачиваемых банку.

Формула и примеры — для экономистов.

Говоря о ставке дисконта, выделяют понятие дисконтирующего множителя (факторного множителя)— ДМi:

.

При определенной ставке дисконта и определенном периоде времени дисконтирующий множитель неизменен.

Дисконтирующий множитель показывает настоящую стоимость одного рубля из некоторой будущей стоимости.

studfiles.net

• 
  Реструктуризация и рефинансирование кредита в чем разница
• 
  Разница между mastercard и visa
• 
  Как отменить платеж в госуслугах если он в обработке
• 
  Мастеркард більше
• 
  Самый выгодный депозит
• 
  Как сменить номер телефона
• 
  Бонусы спасибо где можно списать
• 
  Что делать если подал заявку на ипотеку а процент снизили
• 
  Как снизить процент по кредиту
• 
  Пополнение мобильного
• 
  Пос кредит